题目内容
(2013年四川绵阳4分)二次函数y=ax2+bx+c的图象如图所示,给出下列结论:
①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<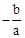 ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.
其中正确的结论是 (写出你认为正确的所有结论序号).
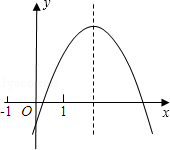
①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<
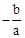 ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.其中正确的结论是 (写出你认为正确的所有结论序号).
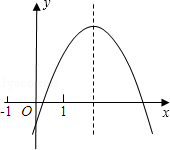
①③④。
∵抛物线开口向下,∴a<0。∴2a<0。
∵对称轴x=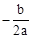 >1,﹣b<2a,∴2a+b>0。故选项①正确。
>1,﹣b<2a,∴2a+b>0。故选项①正确。
∵﹣b<2a,∴b>﹣2a>0>a,
取符合“开口向下,与x轴的一个交点的横坐标在0与1之间,对称轴在直线x=1右侧”的特点的一函数,如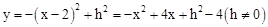 ,
,
令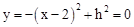 ,得
,得 。
。
由 得
得 。
。
∴ 。
。
当 时,a>c,a<c,a= c都有可能。故②选项错误。
时,a>c,a<c,a= c都有可能。故②选项错误。
∵﹣1<m<n<1,﹣2<m+n<2,
∴抛物线对称轴为:x==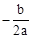 >1,
>1,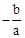 >2,m+n<
>2,m+n<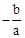 。故选项③正确。
。故选项③正确。
当x=1时,a+b+c>0,2a+b>0,3a+2b+c>0,∴3a+c>﹣2b。∴﹣3a﹣c<2b。
∵a<0,b>0,c<0,∴3|a|+|c|=﹣3a﹣c<2b=2|b|。故④选项正确。
综上所述,正确的结论是①③④。
∵对称轴x=
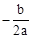 >1,﹣b<2a,∴2a+b>0。故选项①正确。
>1,﹣b<2a,∴2a+b>0。故选项①正确。∵﹣b<2a,∴b>﹣2a>0>a,
取符合“开口向下,与x轴的一个交点的横坐标在0与1之间,对称轴在直线x=1右侧”的特点的一函数,如
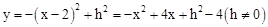 ,
,令
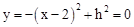 ,得
,得 。
。由
 得
得 。
。∴
 。
。当
 时,a>c,a<c,a= c都有可能。故②选项错误。
时,a>c,a<c,a= c都有可能。故②选项错误。∵﹣1<m<n<1,﹣2<m+n<2,
∴抛物线对称轴为:x==
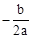 >1,
>1,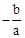 >2,m+n<
>2,m+n<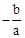 。故选项③正确。
。故选项③正确。当x=1时,a+b+c>0,2a+b>0,3a+2b+c>0,∴3a+c>﹣2b。∴﹣3a﹣c<2b。
∵a<0,b>0,c<0,∴3|a|+|c|=﹣3a﹣c<2b=2|b|。故④选项正确。
综上所述,正确的结论是①③④。

练习册系列答案
相关题目
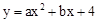 的对称轴是直线x=
的对称轴是直线x= ,与x轴交于点A、B两点,与y轴交于点C,并且点A的坐标为(—1,0).
,与x轴交于点A、B两点,与y轴交于点C,并且点A的坐标为(—1,0).



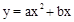 。
。 。
。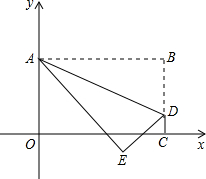
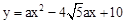 (a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.
(a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围. 中,当x>0时,y随x的增大而增大,则二次函数y=m x2+m x的图象大致是下图中的
中,当x>0时,y随x的增大而增大,则二次函数y=m x2+m x的图象大致是下图中的