��Ŀ����
��2013���Ĵ�����12�֣���ͼ���ı���ABCD��ƽ���ı��Σ�����A��C��D��������y=ax2+bx+c��a��0������x�����һ����ΪE������CE����A��B��D������ֱ�Ϊ����2��0������3��0������0��4����
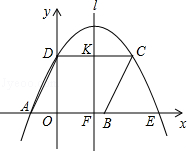
��1���������ߵĽ���ʽ��
��2����֪�����ߵĶԳ���l��x���ڵ�F�����߶�CD�ڵ�K����M��N�ֱ���ֱ��l��x���ϵĶ��㣬����MN�����߶�MNǡ�ñ�BC��ֱƽ��ʱ�����N�����ꣻ
��3�������㣨2���������£�����M��һ��ֱ�ߣ�ʹ֮���ı���AECD�������Ϊ3��4�������֣������ֱ�ߵĽ���ʽ��

��1���������ߵĽ���ʽ��
��2����֪�����ߵĶԳ���l��x���ڵ�F�����߶�CD�ڵ�K����M��N�ֱ���ֱ��l��x���ϵĶ��㣬����MN�����߶�MNǡ�ñ�BC��ֱƽ��ʱ�����N�����ꣻ
��3�������㣨2���������£�����M��һ��ֱ�ߣ�ʹ֮���ı���AECD�������Ϊ3��4�������֣������ֱ�ߵĽ���ʽ��
�⣺��1���ߵ�A��B��D������ֱ�Ϊ����2��0������3��0������0��4�������ı���ABCD��ƽ���ı��Σ�
��AB=CD=5�����C��������5��4����
��������y=ax2+bx+c��a��0������A��C��D��
��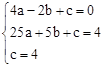 �����]
�����]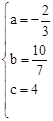 ��
��
�������ߵĽ���ʽΪ ��
��
��2������BD���Գ�����G��

��Rt��OBD������BD=5��
��CD=BD�����DCB=��DBC��
�֡ߡ�DCB=��CBE�����DBC=��CBE��
��G��GN��BC��H����x����N����֤GH=HN��
���G���M�غϡ�
��ֱ��BD�Ľ���ʽ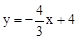 ��
��
���������߿�֪�Գ��᷽��Ϊx=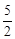 ��
��
���M��������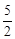 ��
��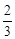 ������GF= MF=
������GF= MF=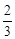 ��BF=
��BF= ��
��
�� ��
��
�֡�MN��BC��ֱƽ�֣���BM=BN=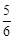 ����BN=OB+BN=3+
����BN=OB+BN=3+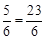 ��
��
���N��������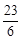 ��0����
��0����
��3������M��ֱ�߽�x���ڵ�P1��
�����ı���AECD�����Ϊ28���ı���ABCD�����Ϊ20��
�ɡ��ı���AECD�������Ϊ3��4����ֱ֪��P1M�����߶�CD�ཻ��
�轻��ΪQ1���ı���AP1Q1D�����ΪS1���ı���P1ECQ1�����ΪS2����P1������Ϊ��a��0������S2=12��
����P�ڶԳ������࣬��P1F=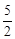 ��a��P1E=7��a��
��a��P1E=7��a��
�ɡ�MKQ1�ס�MFP1���� ����Q1K=5P1F=5��
����Q1K=5P1F=5��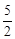 ��a����
��a����
��CQ1=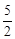 ��5��
��5��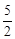 ��a��=5a��10��
��a��=5a��10��
�� ����
����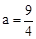 ��
��
����P1�� ��0����M��
��0����M��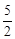 ��
��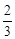 ������ֱ��P1M�Ľ���ʽΪ
������ֱ��P1M�Ľ���ʽΪ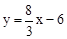 ��
��
����P�ڶԳ�����Ҳ࣬ͬ���ɵ�ֱ��P2M�Ľ���ʽΪ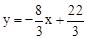 ��
��
������������ֱ�ߵĽ���ʽΪ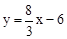 ��
��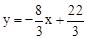 ��
��
��AB=CD=5�����C��������5��4����
��������y=ax2+bx+c��a��0������A��C��D��
��
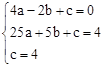 �����]
�����]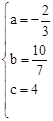 ��
���������ߵĽ���ʽΪ
 ��
����2������BD���Գ�����G��

��Rt��OBD������BD=5��
��CD=BD�����DCB=��DBC��
�֡ߡ�DCB=��CBE�����DBC=��CBE��
��G��GN��BC��H����x����N����֤GH=HN��
���G���M�غϡ�
��ֱ��BD�Ľ���ʽ
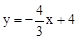 ��
�� ���������߿�֪�Գ��᷽��Ϊx=
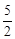 ��
�����M��������
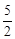 ��
��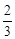 ������GF= MF=
������GF= MF=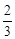 ��BF=
��BF= ��
����
 ��
���֡�MN��BC��ֱƽ�֣���BM=BN=
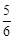 ����BN=OB+BN=3+
����BN=OB+BN=3+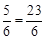 ��
�����N��������
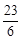 ��0����
��0������3������M��ֱ�߽�x���ڵ�P1��
�����ı���AECD�����Ϊ28���ı���ABCD�����Ϊ20��
�ɡ��ı���AECD�������Ϊ3��4����ֱ֪��P1M�����߶�CD�ཻ��
�轻��ΪQ1���ı���AP1Q1D�����ΪS1���ı���P1ECQ1�����ΪS2����P1������Ϊ��a��0������S2=12��
����P�ڶԳ������࣬��P1F=
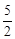 ��a��P1E=7��a��
��a��P1E=7��a���ɡ�MKQ1�ס�MFP1����
 ����Q1K=5P1F=5��
����Q1K=5P1F=5��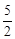 ��a����
��a������CQ1=
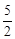 ��5��
��5��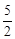 ��a��=5a��10��
��a��=5a��10����
 ����
����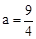 ��
������P1��
 ��0����M��
��0����M��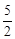 ��
��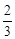 ������ֱ��P1M�Ľ���ʽΪ
������ֱ��P1M�Ľ���ʽΪ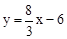 ��
������P�ڶԳ�����Ҳ࣬ͬ���ɵ�ֱ��P2M�Ľ���ʽΪ
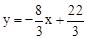 ��
��������������ֱ�ߵĽ���ʽΪ
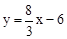 ��
��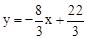 ��
����1������ƽ���ı��ε����ʿ����C�����꣬�ɴ���ϵ����������������ߵĽ���ʽ��
��2������BD���Գ�����G����G��GN��BC��H����x����N�����ݴ���ϵ�����������ֱ��BD�Ľ���ʽ�����������߶Գ��ṫʽ����Գ��ᣬ�ɴ˼��������N�����ꡣ
��3������M��ֱ�߽�x���ڵ�P1���ֵ�P�ڶԳ������࣬��P�ڶԳ�����Ҳ࣬����������ۼ������ֱ�ߵĽ���ʽ��
��2������BD���Գ�����G����G��GN��BC��H����x����N�����ݴ���ϵ�����������ֱ��BD�Ľ���ʽ�����������߶Գ��ṫʽ����Գ��ᣬ�ɴ˼��������N�����ꡣ
��3������M��ֱ�߽�x���ڵ�P1���ֵ�P�ڶԳ������࣬��P�ڶԳ�����Ҳ࣬����������ۼ������ֱ�ߵĽ���ʽ��

��ϰ��ϵ�д�
 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д� �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�����Ŀ
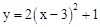 �Ķ��������ǡ� ��
�Ķ��������ǡ� �� ��x�ᡢy��ֱ���A��B���㣬������D��E�ֱ��A��B����ͬʱ������O���˶����˶���O��ֹͣ�����Գ������A�Ҷ���ΪM��������
��x�ᡢy��ֱ���A��B���㣬������D��E�ֱ��A��B����ͬʱ������O���˶����˶���O��ֹͣ�����Գ������A�Ҷ���ΪM�������� ��a��0��ʼ�վ�����E����E��EG��OA���������ڵ�G����AB�ڵ�F������DE��DF��AG��BG����D��E���˶��ٶȷֱ���1����λ����/���
��a��0��ʼ�վ�����E����E��EG��OA���������ڵ�G����AB�ڵ�F������DE��DF��AG��BG����D��E���˶��ٶȷֱ���1����λ����/��� ����λ����/�룬�˶�ʱ��Ϊt�룮
����λ����/�룬�˶�ʱ��Ϊt�룮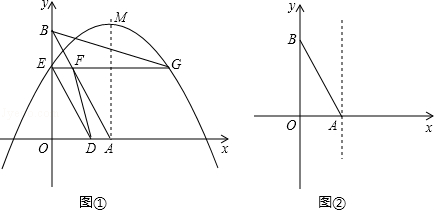
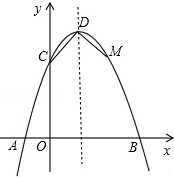
 ��y���ڵ�A����x���������ڵ�B��
��y���ڵ�A����x���������ڵ�B��
 (a��0)��ͼ����x�����������㣬����ֱ�Ϊ(x1��0)��(x2��0)����x1<x2��ͼ������һ��M (x0��y0)��x���·����������ж���ȷ����
(a��0)��ͼ����x�����������㣬����ֱ�Ϊ(x1��0)��(x2��0)����x1<x2��ͼ������һ��M (x0��y0)��x���·����������ж���ȷ���� ����3|a|+|c|��2|b|��
����3|a|+|c|��2|b|��

