Question

如图，△ABC中，AD是BC上的高，AE平分∠BAC，∠B=75°，∠C=45°，求∠DAE与∠AEC的度数．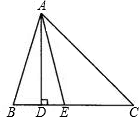

Answer 1

方法1：
∵∠B+∠C+∠BAC=180°，∠B=75°，∠C=45°，
∴∠BAC=60°，
∵AE平分∠BAC，
∴∠BAE=∠CAE=

1

2

∠BAC=

1

2

×60°=30°，
∵AD是BC上的高，
∴∠B+∠BAD=90°，
∴∠BAD=90°-∠B=90°-75°=15°，
∴∠DAE=∠BAE-∠BAD=30°-15°=15°，
在△AEC中，∠AEC=180°-∠C-∠CAE=180°-45°-30°=105°；

方法2：同方法1，得出∠BAC=60°．
∵AE平分∠BAC，
∴∠EAC=

1

2

∠BAC=

1

2

×60°=30°．
∵AD是BC上的高，
∴∠C+∠CAD=90°，
∴∠CAD=90°-45°=45°，
∴∠DAE=∠CAD-∠CAE=45°-30°=15°．
∵∠AEC+∠C+∠EAC=180°，
∴∠AEC+30°+45°=180°，
∴∠AEC=105°．
答：∠DAE=15°，∠AEC=105°．