Question

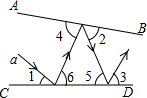
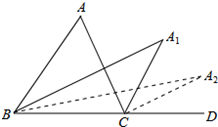
如图，在△ABC中，∠A=m°，∠ABC和∠ACD的平分线交于点A₁，得∠A₁；∠A₁BC和∠A₁CD的平分线交于点A₂，得∠A₂；…∠A₂₀₁₂BC和∠A₂₀₁₂CD的平分线交于点A₂₀₁₃，则：
（1）∠A₁=______度；
（2）∠A₂₀₁₃=______度．

Answer 1

（1）由三角形的外角性质得，∠A+∠ABC=∠ACD，∠A₁+∠A₁BC=∠A₁CD，
∵∠ABC和∠ACD的平分线交于点A₁，
∴∠A₁BC=

1

2

∠ABC，∠A₁CD=

1

2

∠ACD，
∴∠A₁+∠A₁BC=

1

2

（∠A+∠ABC），
∴∠A₁=

1

2

∠A，
∵∠A=m°，
∴∠A₁=

1

2

m°；

（2）同理可得：∠A₂=

1

2

∠A₁=

1

22

∠A，
∠A₃=

1

2

∠A₂=

1

23

∠A，
…，
∠A₂₀₁₃=

1

22013

∠A，
∵∠A=m°，
∴∠A₂₀₁₃=

1

22013

m°．
故答案为：

1

2

m；

1

22013

m．