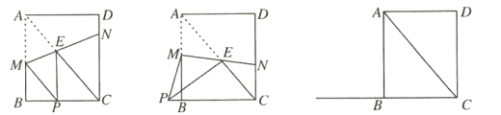
��Ŀ����
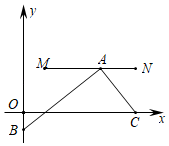
����Ŀ����ͼ����ֱ֪��y��x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y����x2+bx+c����A��B���㣬��x�ύ����һ����C���Գ�����ֱ��AB���ڵ�E�������߶���ΪD��
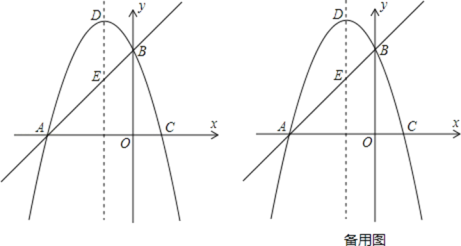
��1����A�������� ������B�������� ����
��2�����������ߵĽ���ʽ��
��ֱ��AB�������ߵĶԳ��ύ�ڵ�E����x�����Ƿ���ڵ�M��ʹ��ME+MB��С�������M�����꣮
��3����P�ӵ�D�������ضԳ���������ÿ��1����λ���ȵ��ٶ������˶������˶���ʱ��Ϊt�룬��tΪ��ֵʱ����P��B��CΪ������������ǵ��������Σ�ֱ��д�����з���������tֵ��
���𰸡���1������3��0������0��3������2����y����x2��2x+3����M����![]() ��0������3����tΪ3��4��
��0������3����tΪ3��4��![]() ��4��ʱ����P��B��CΪ������������ǵ���������
��4��ʱ����P��B��CΪ������������ǵ���������
��������
��1����x��0����y��3����y��0����x����3��������⣻
��2����B������Ϊ����0��3������c��3������A��������������߱���ʽ����ã�b����2��������⣻
�ں����ĶԳ���Ϊ��x����1����E����1��2������B��0��3��������B����x��ĶԳƵ�B����0����3��������EB����x���ڵ�M�����MΪ��������⣻
��3����PC��PB��BC��PC��BC��PB������������ֱ���⼴�ɣ�
�⣺��1��y��x+3����x��0����y��3����y��0����x����3��
�ʵ�A��B������ֱ�Ϊ������3��0������0��3����
�ʴ�Ϊ������3��0������0��3����
��2����B����������0��3������c��3��
����A��������������߱���ʽy����x2+bx+3�еã�-(-3)2-3b+3=0
��ã�b����2��
�������ߵĽ���ʽΪy����x2��2x+3��
�ں����ĶԳ���Ϊ��x����1
��x=-1�������ʽy��x+3��y=-1+3=2
���E����1��2������B��0��3����
����B����x��ĶԳƵ�B����0����3��������EB����x���ڵ�M�����MΪ����
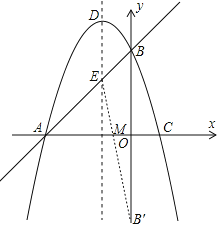
��ֱ��B��E�ı���ʽΪy=mx+n
��B����0����3����E����1��2������ã�
![]()
���![]()
��ֱ��B��E�ı���ʽΪ��y����5x��3��
��y��0ʱ��x����![]() ���ʵ�M����
���ʵ�M����![]() ��0����
��0����
��3����y����x2��2x+3��y��0����x2��2x+3������x��1����x+3����0��
��ã�x��1��x����3��
��C��1��0����
��y����x2��2x+3������x+1��2+4��
��D����1��4����P����1��4��t����
��B��0��3����C��1��0����
��PC2������1��1��2+��4��t��2��t2��8t+20��PB2������1��2+��4��t��3��2��t2��2t+2��BC2��12+32��10��
�ٵ�PC��PBʱ��
��t2��8t+20��t2��2t+2��ã�t��3��
�ڵ�BC��PCʱ��
��100= t2��8t+20��ã�t��4��![]() ��
��
�۵�BC��PBʱ��
��100= t2��2t+2��ã�t��4��2����ȥ��ֵ��
���Ͽ�֪����tΪ3��4��![]() ��4��ʱ����P��B��CΪ������������ǵ��������Σ�
��4��ʱ����P��B��CΪ������������ǵ��������Σ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij���˾��A��B����Ӫ����͡�һ�죬��˾�۳����ֿ��640�ݣ�����2160Ԫ�����ֿ�͵ijɱ��ۡ����ۼ����±���
A�ֿ�� | B�ֿ�� | |
�ɱ��� | 5Ԫ/�� | 6Ԫ/�� |
���ۼ� | 8Ԫ/�� | 10Ԫ/�� |
��1����ù�˾��һ������A��B���ֿ�����ٷݣ�
��2��Ϊ�������ۣ���˾�����ڶ����һ��������A��B���ֿ��ͬʱ���н��۴���������۵�A��B���ֿ�͵�������Ϊ��һ������A��B���ֿ��������2������A�ֿ�Ͱ�ԭ���ۼ۵ľ����۳��ۣ�����˾Ҫ����Щ��͵���ȫ���۳����������������3280Ԫ����ôB�ֿ����Ϳ���ԭ���ۼ۴��۳��ۣ�