题目内容
【题目】（1）已知某抛物线与抛物线y＝﹣2x2+3x﹣1的形状和开口方向都相同，并且其对称轴为x＝1，函数的最大值为4，求此抛物线的解析式；
（2）已知一个二次函数图象经过（﹣1，10），（1，4），（2，7）三点，求它的解析式；
（3）某抛物线过点（1，0），（﹣2，0）并且与直线y＝2x﹣1的交点的纵坐标为5，求此抛物线的解析式．
【答案】（1）y＝﹣2x2+4x+2；（2）y＝2x2﹣3x+5；（3）
．
【解析】
（1）根据抛物线的形状，开口方向与抛物线y=-2x2+3x-1的形状和开口方向都相同，可知a的值，又知抛物线的顶点即可求出解析式；
（2）设二次函数的解析式为y=ax2+bx+c，把（-1，10），（1，4），（2，7）三点坐标代入，列方程组求a、b、c的值，确定函数解析式；
（3）设抛物线的解析式为y=a（x-1）（x+2），求出抛物线与直线的交点为（3，5），将（3，5）代入抛物线解析式可得a的值．
解：（1）∵抛物线y＝﹣2x2+3x﹣1的形状和开口方向都相同，
∴所求抛物线解析式y＝﹣2（x﹣h）2+k，
又∵对称轴为x＝1，函数的最大值为4，
∴抛物线的解析式为y＝﹣2（x﹣1）2+4，即y＝﹣2x2+4x+2；
（2）设二次函数的解析式为y＝ax2+bx+c，把（﹣1，10），（1，4），（2，7）各点代入上式得：
，
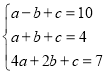解得：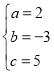
．
∴抛物线解析式为y＝2x2﹣3x+5；
（3）∵抛物线过点（1，0），（﹣2，0），
∴设抛物线的解析式为y＝a（x﹣1）（x+2），
抛物线与直线y＝2x﹣1的交点的纵坐标为5，
∴5＝2x﹣1，
解得：x＝3，
∴抛物线与直线y＝2x﹣1的交点坐标为（3，5），
将（3，5）代入抛物线解析式可得a（3﹣1）（3+2）＝5，
∴a＝
，
∴抛物线的解析式为y＝（x﹣1）（x+2），即．
