题目内容
【题目】如图,将半径为3cm,圆心角为60°的扇形纸片.AOB在直线l上向右作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长 cm(结果保留π).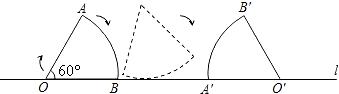
【答案】4π
【解析】解:顶点O经过的路线可以分为三段,
第一段:当弧AB切直线l于点B时,有OB⊥直线l,此时O点绕不动点B转过了90°.
此时点O经过了以O为圆心,以3为半径的圆的周长的 ![]() ,即经过了
,即经过了 ![]() ×2π×3=
×2π×3= ![]() ;
;
第二段:OB⊥直线l到OA⊥直线l,O点绕动点转动,而这一过程中弧AB始终是切于直线l的,
所以O与转动点的连线始终⊥直线l,
所以O点在水平运动,此时O点经过的路线长=BA’=AB的弧长= ![]() =π;
=π;
第三段:OA⊥直线l到O点落在直线l上,O点绕不动点A转过了90°,
此时点O经过了以O为圆心,以3为半径的圆的周长的 ![]() ,即经过了
,即经过了 ![]() ×2π×3=
×2π×3= ![]() ;
;
所以,O点经过的路线总长S= ![]() +π+
+π+ ![]() =4π.
=4π.
所以答案是4π.
【考点精析】本题主要考查了圆心角、弧、弦的关系和弧长计算公式的相关知识点,需要掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的才能正确解答此题.

练习册系列答案
相关题目