题目内容
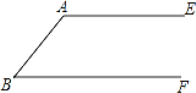
【题目】如图,AE∥BF,先按(1)的要求作图,再按(2)的要求证明
(1)用直尺和圆规作出∠ABF的平分线BD交AE于点D,再作出BD的中点O(不写作法,保留作图痕迹)
(2)连接(1)所作图中的AO并延长与BF相交于点C,连接DC,求证:四边形ABCD是菱形.
【答案】(1)、答案见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据角平分线的作法和中点的作法得出答案;(2)、首先证明△ADO与△CBO全等,从而得出四边形ABCD为平行四边形,然后根据BD平分∠ABC得出∠ABD=∠CBD,根据AE∥BF得出∠ABD=∠ADB,从而得出AB=AD,根据点O是BD的中点得出对角线互相垂直,从而得出菱形.
试题解析:(1)、如图.
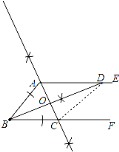
(2)、∵AE∥BF,∴∠ADO=∠CBO.在△ADO与△CBO中,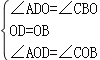 ,
,
∴△ADO≌△CBO(ASA),∴AD=BC, ∴四边形ABCD是平行四边形.
∵BD平分∠ABC,∴∠ABD=∠CBD.又∵AE∥BF,
∴∠ABD=∠ADB,∴AB=AD.又∵点O是BD的中点,∴AO⊥BD,即AC⊥BD.
∴平行四边形ABCD是菱形.

练习册系列答案
相关题目
【题目】下表是某水库一周内水位高低的变化情况(用正数记水位比前一日上升数,用负数记下降数).那么本周星期几水位最低( )
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/米 | 0.12 | ﹣0.02 | ﹣0.13 | ﹣0.20 | ﹣0.08 | ﹣0.02 | 0.32 |
A. 星期二 B. 星期四 C. 星期六 D. 星期五