Question

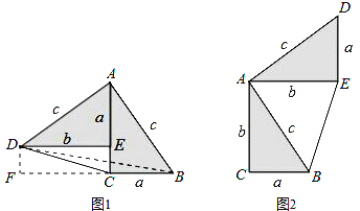
【题目】如图，等腰Rt△ABC中，∠BAC=90°，AD⊥BC于D，∠ABC的平分线分别交AC、AD于E、F两点，M为EF的中点，延长AM交BC于点N，连接DM．下列结论：①DF=DN ②AE=CN；③△DMN是等腰三角形；④∠BMD=45°，其中正确的结论个数是 ( )

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】D

【解析】试题分析：求出BD=AD，∠DBF=∠DAN，∠BDF=∠ADN，证△DFB≌△DAN，即可判断①，证△ABF≌△CAN，推出CN=AF=AE，即可判断②；根据A、B、D、M四点共圆求出∠ADM=22.5°，即可判断④，根据三角形外角性质求出∠DNM，求出∠MDN=∠DNM，即可判断③．

解：∵∠BAC=90°，AC=AB，AD⊥BC，

∴∠ABC=∠C=45°，AD=BD=CD，∠ADN=∠ADB=90°，

∴∠BAD=45°=∠CAD，

∵BE平分∠ABC，

∴∠ABE=∠CBE=∠ABC=22.5°，

∴∠BFD=∠AEB=90°﹣22.5°=67.5°，

∴∠AFE=∠BFD=∠AEB=67.5°，

∴AF=AE，

∵M为EF的中点，

∴AM⊥BE，

∴∠AMF=∠AME=90°，

∴∠DAN=90°﹣67.5°=22.5°=∠MBN，

在△FBD和△NAD中

∴△FBD≌△NAD，

∴DF=DN，∴①正确；

在△AFB和△△CNA中

∴△AFB≌△CAN，

∴AF=CN，

∵AF=AE，

∴AE=CN，∴②正确；

∵∠ADB=∠AMB=90°，

∴A、B、D、M四点共圆，

∴∠ABM=∠ADM=22.5°，

∴∠DMN=∠DAN+∠ADM=22.5°+22.5°=45°，∴④正确；

∵∠DNA=∠C+∠CAN=45°+22.5°=67.5°，

∴∠MDN=180°﹣45°﹣67.5°=67.5°=∠DNM，

∴DM=MN，∴△DMN是等腰三角形，∴③正确；

即正确的有4个，

故选D．