题目内容
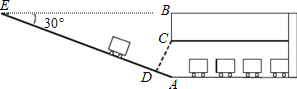
【题目】某校九年级数学兴趣小组为了测得该校地下停车场的限高CD，在课外活动时间测得下列数据：如图，从地面E点测得地下停车场的俯角为30°，斜坡AE的长为16米，地面B点（与E点在同一个水平线）距停车场顶部C点（A、C、B在同一条直线上且与水平线垂直）1.2米．试求该校地下停车场的高度AC及限高CD（结果精确到0.1米,
=1.732）．
【答案】AC=6.8米；CD=5.9米
【解析】
试题分析：首先根据题意得出AB=8米，从而得出AC的长度，然后根据三角函数得出CD的长度.
试题解析：由题意得，AB⊥EB，CD⊥AE，∴∠CDA=∠EBA=90°，
∵∠E=30°，∴AB=
AE=8米，
∵BC=1.2米，∴AC=AB﹣BC=6.8米，
∵∠DCA=90°﹣∠A=30°，∴CD=AC×cos∠DCA=6.8×
≈5.9米．
答：该校地下停车场的高度AC为6.8米，限高CD约为5.9米．
练习册系列答案
相关题目
【题目】为节约用水,某市居民生活用水按级收费,具体收费标准如下表：
用水量（吨） | 不超过15吨的部分 | 超过15不超过25吨的部分 | 超过25吨的部分 |
单位（元/吨） | 3 | 5 | 7 |
设李红家某月的为x吨(15<x25)，应付水费为y元，则y关于x的函数表达式为_______．
