Question

【题目】如图，等边外有一点，连接，，.

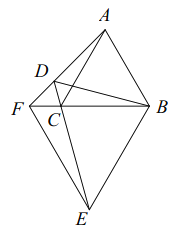
图1 图2 图3

（1）如图1，若，求证：平分；

（2）如图2，若，求证：；

（3）如图3，延长交的延长线于点，以为边向下作等边，若点，，在同一直线上，且，直接写出的度数为___________（结果用含的式子表示）.

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）

【解析】

（1）过点作于点，于点，证明，即可证明；

（2）在上取点，使，得到为等边三角形，再证明，得到，即可证明；

（3）先根据等边三角形的性质证明△ABF≌CBE，得到∠1=∠2，再得到，由（1）得,再得到F,E,B,D四点共圆，得到∠3=∠DBF即可求解.

（1）过点作于点，于点，

∵

又

∴

又BC=BA

∴（AAS）

，

平分；

（2）在上取点，使，

∵

为等边三角形，

∴∠DCE=∠ACB=60°，

∵∠DCE-∠ACE =∠ACB-∠ACE

∴∠DCA=∠ECB

又DC=EC,AC=BC

∴，

，

∴BD-CD=BD-DE=BE=AD

；

（3）如图，∵△ABC，△BEF为等边三角形，

∴AB=CB,BF=BE,∠ABF=∠CBE

∴△ABF≌CBE，

∴∠1=∠2，

∵∠2+∠3=60°，∠4=60°

∴∠FDE=180°-∠1-∠4-∠3=60°

∴∠ADC=120°，

∴，

由（1）得平分

∴,

∴∠FDB=120°，

∴∠FDB+∠FEB=180°，

∴F,E,B,D四点共圆，

∴∠3=∠DBF

∵∠DBF=60°-

∴∠3=.

故答案为.