Question

【题目】已知矩形，，，将它绕着点按顺时针方向旋转度得到矩形，此时，这两边所在的直线分别与边所在的直线相交于点、，当时，的长为________．

Answer 1

【答案】

【解析】

作PH⊥C1D1（如图），证明∴△BPC≌△PQH，根据全等三角形的性质得到PQ=PB，又因DP：DQ=1：2，所以DP=BP=PQ；设DP=x，则BP=x，PC=DC-DP=8-x，在Rt△BCP中，利用勾股定理可得方程（8-x）2+42=x2，解方程求得x=5，即可求得DP的长.

作PH⊥C1D1，如图，

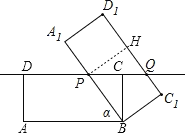
∵矩形ABCD绕着点B按顺时针方向旋转得到矩形A1BC1D1，

∴BC=BC1=4，

易得四边形BPHC1为矩形，

∴PH=BC1，

∴BC=PH，

∵C1D1∥A1B，

∴∠BPC=∠PQH，

在△BPC和△PQH中， ，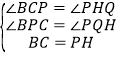

∴△BPC≌△PQH，

∴PQ=PB，

∵DP：DQ=1：2，

∴DP=BP=PQ，

设DP=x，则BP=x，PC=DC-DP=8-x，

在Rt△BCP中，（8-x）2+42=x2，解得x=5，

即DP的长为5．

故答案为：5．