题目内容
【题目】已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC,在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.
(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;
(2)当点P在射线BA上时,设![]() ,求y关于
,求y关于![]() 的函数解析式及定义域;
的函数解析式及定义域;
(3)联结PQ,直线PQ与直线BC交于点E,如果![]() 与
与![]() 相似,求线段BP的长.
相似,求线段BP的长.

【答案】(1)![]() ;(2)
;(2)![]() (
(![]() );(3)
);(3)![]() 或
或![]()
【解析】
(1)如图1中,作PH⊥BC于H.解直角三角形求出BH,PH,在Rt△PCH中,由勾股定理即可解决问题.
(2)如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.证明△POQ∽△BOC,推出∠OPQ=∠OBC=30°=∠PCQ,推出PQ=CQ=y,推出PC=![]() y,在Rt△PHB中,BH=
y,在Rt△PHB中,BH=![]() x,PH=
x,PH=![]() x,根据PC2=PH2+CH2,可得结论.
x,根据PC2=PH2+CH2,可得结论.
(3)分以下几种情形:①如图2中,若直线QP交直线BC于B点左侧于E.②如图3中,若直线QP交直线BC于C点右侧于E.③如图④中,点P在AB的延长线上,直线PQ与BC的交点E在线段BC上.分别求解即可.
解:(1)如图1中,作PH⊥BC于H.
∵四边形ABCD是菱形,
∴AB=BC=4,AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=120°,
∴∠PBH=60°,
∵PB=3,∠PHB=90°,
∴BH=PBcos60°=![]() ,PH=PBsin60°=
,PH=PBsin60°=![]() ,
,
∴CH=BC-BH=4-![]() =
=![]() ,
,
∴PC=![]() =
=![]() .
.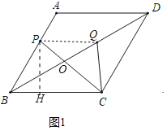
(2)如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.
∵四边形ABCD是菱形,
∴∠ABD=∠CBD=30°,
∵∠PCQ=30°,
∴∠PBO=∠QCO,
∵∠POB=∠QOC,
∴△POB∽△QOC,
∴![]() ,
,
∴![]() ,
,
∵∠POQ=∠BOC,
∴△POQ∽△BOC,
∴∠OPQ=∠OBC=30°=∠PCQ,
∴PQ=CQ=y,
∴PC=![]() y,
y,
在Rt△PHB中,BH=![]() x,PH=
x,PH=![]() x,
x,
∵PC2=PH2+CH2,
∴3y2=(![]() x)2+(4-
x)2+(4-![]() x)2,
x)2,
∴y=![]() (0≤x<8).
(0≤x<8).
(3)①如图2中,若直线QP交直线BC于B点左侧于E.
此时∠CQE=120°,
∵∠PBC=60°,
∴△PBC中,不存在角与∠CQE相等,
此时△QCE与△BCP不可能相似.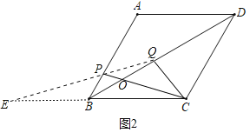
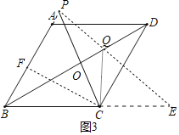
②如图3中,若直线QP交直线BC于C点右侧于E.
则∠CQE=∠ABC=∠QBC+∠QCP=60°=∠CBP,
∵∠PCB>∠E,
∴只可能∠BCP=∠QCE=75°,
作CF⊥AB于F,则BF=2,CF=2![]() ,∠PCF=45°,
,∠PCF=45°,
∴PF=CF=2![]() ,
,
此时PB=2+2![]() .
.
③如图4中,若点P在AB的延长线上,直线PQ与BC的交点E在线段BC上,
因为∠EQC=∠PBC=120°,
要使![]() 与
与![]() 相似,
相似,
只有∠QCE=∠PCE=15°,
此时∠BPC=45°,
过点C作CF⊥AB于F,
可得BF=2,CF=2![]() =PF,
=PF,
此时PB=PF-BF=2![]() -2.
-2.
综上所述,满足条件的PB的值为2+2![]() 或2
或2![]() -2.
-2.

 计算高手系列答案
计算高手系列答案【题目】为庆祝建国70周年,某校举办了爱我中华知识竞赛活动.该校南、北两个校区七年级各有300名学生参加竞赛活动.为了解这两个校区参赛学生成绩情况,从中各随机抽取了10名学生的成绩进行调查,过程如下:
(收集、整理、描述数据)根据随机抽取的10名学生的成绩,制作了如下统计图表:
(说明:成绩90分及以上为优秀,80-89分为良好,60-79分为合格,60分以下为不合格)
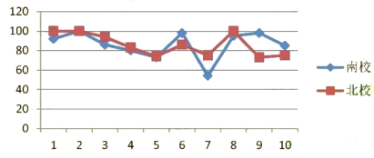
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
南校 | 92 | 100 | 86 | 80 | 73 | 98 | 54 | 95 | 98 | 85 |
北校 | 100 | 100 | 94 | 83 | 74 | 86 | 75 | 100 | 73 | 75 |
(分析数据)对上述数据进行分析,分别求出了两组样本数据的平均数、中位数、众数如下表:
校区 | 平均数(分) | 中位数(分) | 众数(分) |
南校 | 87 | 90.5 | |
北校 | 86 | 100 |
(得出结论)综合上述统计全过程,回答下列问题:
(1)补全表格.
(2)估计北校七年级学生竞赛成绩为优秀的人数.
(3)你认为哪个校区的七年级学生竞赛成绩比较好?说明你的理由.(从两个不同的角度说明推断的合理性)
【题目】安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全区范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽部分使用电瓶车的市民,就骑电瓶车戴安全帽情况(![]() :每次戴、
:每次戴、![]() :经常戴、
:经常戴、![]() :偶尔戴、
:偶尔戴、![]() :都不戴)进行问卷调查,将相关的数据制成如下统计图表.
:都不戴)进行问卷调查,将相关的数据制成如下统计图表.
活动前骑电瓶车戴安全帽情况统计表
类别 | 人数 |
| 68 |
| 245 |
| 510 |
| 177 |
合计 | 1000 |
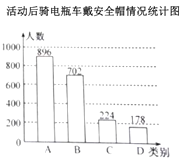
(1)宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
(2)该区约有37万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;
(3)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,谈谈你对交警部门宣传活动的效果的看法.