题目内容
【题目】在平行四边形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() .
.
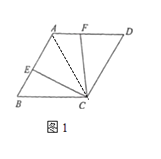
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
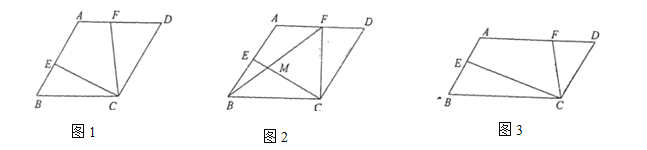
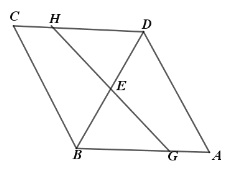
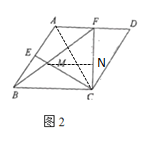
(2)如图2,若![]() ,且点
,且点![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,求
,求![]() ;
;
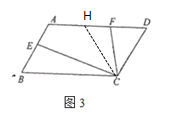
(3)如图3,若![]() ,探究线段
,探究线段![]() 、
、![]() 、
、![]() 三之间的数量关系,说明理由.
三之间的数量关系,说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接AC,根据题意判定平行四边形ABCD为菱形,△ABC为等边三角形,然后利用AAS定理判定△BCE≌△ACF,从而得出BE=AF,使问题得解;
(2)连接AC,过点M作MN⊥CF,由含30°直角三角形的性质求得![]() ,
,![]() ,设CN=x,则
,设CN=x,则![]() ,然后利用平行判定△FMN∽△FBC,根据相似三角形的性质求得
,然后利用平行判定△FMN∽△FBC,根据相似三角形的性质求得![]() ,然后利用勾股定理求解即可;
,然后利用勾股定理求解即可;
(3)连接AC,过点A作AK⊥BC,在DA上截取DH=CD,根据有一个角是60°的等腰三角形是等边三角形判定△HCD是等边三角形,然后根据AA定理判定△BCE ∽△FCH,根据相似三角形的性质求得![]() ,即HF=kBE,从而使问题得解.
,即HF=kBE,从而使问题得解.
解:(1)连接AC
因为在平行四边形ABCD中,![]() ,
,![]()
∴平行四边形ABCD为菱形,△ABC为等边三角形
∴AC=BC,∠B=∠BAC=∠DAC=∠ACB=60°,
又∵![]()
∴∠ACE+∠BCE=∠ACE+∠ACF
∴∠BCE=∠ACF
∴△BCE≌△ACF
∴BE=AF
∴AB=AE+BE=![]()
(2)连接AC,过点M作MN⊥CF
由(1)已证,△ABC为等边三角形,△BCE≌△ACF
∵![]() 为
为![]() 的中点
的中点
∴CE⊥AB
∴在Rt△BCE中,∠BCE=30°
∴![]() ,
,![]()
由题意![]() ,∴∠BCF=90°
,∴∠BCF=90°
在Rt△AMCN中,∠CMN=30°
设CN=x,则![]()
∵MN⊥CF
∴MN∥BC
∴△FMN∽△FBC
∴![]() ,
,![]()
解得:![]()
∴![]()
在Rt△FMN中,![]()
(3)由题意可知,在平行四边形ABCD中,∠B=∠D=60°,![]()
连接AC,过点A作AK⊥BC,在DA上截取DH=CD
∵DH=CD,∠B=∠D=60°
∴△HCD是等边三角形
∴∠HCD=60°
又∵∠ECF=60°
∴∠BCE+∠ECH=∠FCH+∠ECH
∴∠BCE =∠FCH
∴△BCE ∽△FCH
∴![]() ,即HF=kBE
,即HF=kBE
∴CD=DF+HF=DF+ kBE
又∵![]()
∴![]()