��Ŀ����
����Ŀ�������⣩��n��2��1���Σ���Ƕһ��2��n���Σ��ж����ֲ�ͬ����Ƕ��������2��n���α�ʾ���ε��ڱ���2��n��
��̽��������������an�ֲ�ͬ����Ƕ������Ϊ̽��an�ı仯���ɣ����Dz�ȡһ���������⻯�IJ��ԣ��ȴ�����������֣�����εݽ���������ó����ۣ�
̽��һ����1��2��1���Σ���Ƕһ��2��1���Σ��ж����ֲ�ͬ����Ƕ������
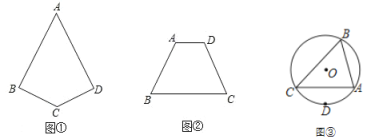
��ͼ��1������Ȼֻ��1����Ƕ���������ԣ�a1��1��
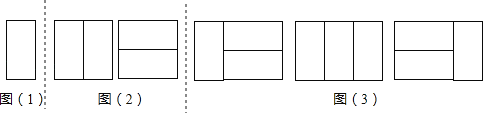
̽��������2��2��1���Σ���Ƕһ��2��2���Σ��ж����ֲ�ͬ����Ƕ������
��ͼ��2������Ȼֻ��2����Ƕ���������ԣ�a2��2��
̽��������3��2��1���Σ���Ƕһ��2��3���Σ��ж����ֲ�ͬ����Ƕ������
һ�ࣺ��̽��һÿ����Ƕͼ���Ҳ��ٺ�����Ƕ2��2��1���Σ���1����Ƕ������
���ࣺ��̽����ÿ����Ƕͼ���Ҳ���������Ƕ1��2��1���Σ���2����Ƕ������
��ͼ��3�������ԣ�a3��1+2��3��
̽���ģ���4��2��1���Σ���Ƕһ��2��4���Σ��ж����ֲ�ͬ����Ƕ������
һ�ࣺ��̽����ÿ����Ƕͼ���Ҳ��ٺ�����Ƕ2��2��1���Σ����� ������Ƕ������
���ࣺ��̽����ÿ����Ƕͼ���Ҳ���������Ƕ1��2��1���Σ����� ������Ƕ������
���ԣ�a4���� ����
̽���壺��5��2��1���Σ���Ƕһ��2��5���Σ��ж����ֲ�ͬ����Ƕ������
����������������д��̽�����̣����û�ͼ��
����
�����ۣ���n��2��1���Σ���Ƕһ��2��n���Σ��ж����ֲ�ͬ����Ƕ������
��ֱ��д��an��an��1��an��2�Ĺ�ϵʽ����д�����̣���
��Ӧ�ã���10��2��1���Σ���Ƕһ��2��10���Σ����� ���ֲ�ͬ����Ƕ������
���𰸡���1��2��3��5����2��an��an��1+an��2����3��89.
��������
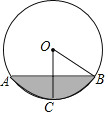
̽���ģ���ͼ����˵����a4=2+3=5��
̽���壺ͬ����̽����ÿ����Ƕͼ���Ҳ��ٺ�����Ƕ2��2��1���κ�̽����ÿ����Ƕͼ���Ҳ���������Ƕ��1��2��1���Σ���ӿɵý��ۣ�
���ۣ�����̽���ĺ���ɵù��ɣ�an=an-1+an-2��
Ӧ�ã����ý������λ�������С��־��Ϊ5��4������̽���ĺ����ֵ����ɵý��ۣ�
�⣺̽���ģ�
��ͼ4��ʾ��

һ�ࣺ��̽����ÿ����Ƕͼ���Ҳ��ٺ�����Ƕ2��2��1���Σ���2����Ƕ������
���ࣺ��̽����ÿ����Ƕͼ���Ҳ���������Ƕ1��2��1���Σ���3����Ƕ������
���ԣ�a4��2+3��5��
�ʴ�Ϊ2��3��5��
̽���壺
һ�ࣺ��̽����ÿ����Ƕͼ���Ҳ��ٺ�����Ƕ2��2��1���Σ���3����Ƕ������
���ࣺ��̽����ÿ����Ƕͼ���Ҳ���������Ƕ1��2��1���Σ���5����Ƕ������
���ԣ�a5��3+5��8��
����
���ۣ�an��an��1+an��2��
Ӧ�ã�a10��a9+a8��a7+a8+a8��2a8+a7��2��a7+a6��+a7��3a7+2a6��3��a6+a5��+2a6��5a6+3a5��5��a5+a4��+3a5��8a5+5a4��8��8+5��5��89��
�ʴ�Ϊ89��