题目内容
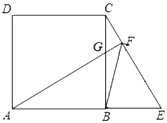
【题目】如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)若AF=10,BC=4![]() ,求tan∠BAD的值.
,求tan∠BAD的值.
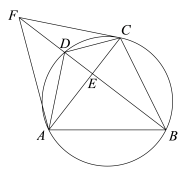
【答案】(1)见解析;(2) tan∠BAD=![]() .
.
【解析】
(1)根据等腰三角形的性质得出∠ABC=∠ACB,根据圆心角、弧、弦的关系得到![]() =
=![]() ,即可得到∠ABC=∠ADB,根据三角形内角和定理得到∠ABC=
,即可得到∠ABC=∠ADB,根据三角形内角和定理得到∠ABC=![]() (180°∠BAC)=90°
(180°∠BAC)=90°![]() ∠BAC,∠ADB=90°∠CAD,从而得到
∠BAC,∠ADB=90°∠CAD,从而得到![]() ∠BAC=∠CAD,即可证得结论;
∠BAC=∠CAD,即可证得结论;
(2)易证得BC=CF=4![]() ,即可证得AC垂直平分BF,证得AB=AF=10,根据勾股定理求得AE、CE、BE,根据相交弦定理求得DE,即可求得BD,然后根据三角形面积公式求得DH,进而求得AH,解直角三角形求得tan∠BAD的值.
,即可证得AC垂直平分BF,证得AB=AF=10,根据勾股定理求得AE、CE、BE,根据相交弦定理求得DE,即可求得BD,然后根据三角形面积公式求得DH,进而求得AH,解直角三角形求得tan∠BAD的值.
解:(1)∵AB=AC,
∴![]() =
=![]() ,∠ABC=∠ACB,
,∠ABC=∠ACB,
∴∠ABC=∠ADB,∠ABC=![]() (180°∠BAC)=90°
(180°∠BAC)=90°![]() ∠BAC,
∠BAC,
∵BD⊥AC,
∴∠ADB=90°∠DAC,
∴![]() ∠BAC=∠DAC,
∠BAC=∠DAC,
∴∠BAC=2∠DAC;
(2)∵DF=DC,
∴∠BFC=![]() ∠BDC=
∠BDC=![]() ∠BAC=∠FBC,
∠BAC=∠FBC,
∴CB=CF,
又BD⊥AC,
∴AC是线段BF的中垂线,AB= AF=10, AC=10.
又BC=4![]() ,
,
设AE=x, CE=10-x,
AB2-AE2=BC2-CE2, 100-x2=80-(10-x)2, x=6
∴AE=6,BE=8,CE=4,
∴DE=![]() =
=![]() =3,
=3,
∴BD/span>=BE+DE=3+8=11,
作DH⊥AB,垂足为H,
∵![]() ABDH=
ABDH=![]() BDAE,
BDAE,
∴DH=![]() ,
,
∴BH=![]() ,
,
∴AH=ABBH=10![]() ,
,
∴tan∠BAD=![]() =
=![]() =
=![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目