题目内容
已知抛物线 与
与 轴相交于
轴相交于 ,
, 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴相交于点
轴相交于点 .
.
(1)点 的坐标为 ,点
的坐标为 ,点 的坐标为 ;
的坐标为 ;
(2)在 轴的正半轴上是否存在点
轴的正半轴上是否存在点 ,使以点
,使以点 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出点
相似?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(1)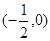 ,
,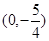 ;(2)存在,
;(2)存在,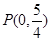 或
或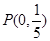 .
.
解析试题分析:(1)令y=0,解关于x的一元二次方程求出A、B的坐标,令x=0求出点C的坐标,再根据顶点坐标公式计算即可求出顶点D的坐标;
(2)根据点A、C的坐标求出OA、OC的长,再分OA和OA是对应边,OA和OC是对应边两种情况,利用相似三角形对应边成比例列式求出OP的长,从而得解;
试题解析:(1)点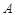 的坐标为
的坐标为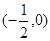 ,点
,点 的坐标为
的坐标为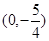
(2)在 轴的正半轴上存在符合条件的点
轴的正半轴上存在符合条件的点 ,设点
,设点 的坐标为
的坐标为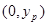
∵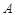
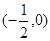 ,
,
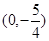 ,
,
∴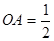 ,
,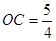 ,
,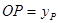 .
.
∵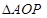 ∽
∽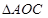 ,
,
∴ ,
,
∴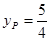 ,
,
∴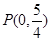 .
.
∵ ∽
∽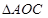 ,
,
∴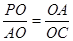 ,
,
∴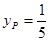 ,
,
∴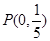 .
.
∴符合条件的点 有两个,
有两个,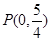 或
或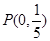 .
.
考点: 二次函数综合题.

练习册系列答案
相关题目
 轴建立直角坐标系,桥洞上沿形状恰好是抛物线
轴建立直角坐标系,桥洞上沿形状恰好是抛物线 的图像.桥洞两侧壁上各有一盏距离水面4米高的景观灯.请求出这两盏景观灯间的水平距离.
的图像.桥洞两侧壁上各有一盏距离水面4米高的景观灯.请求出这两盏景观灯间的水平距离.

 的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交
的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交 轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
 轴上的点(0,6)时,求此时D点的坐标;
轴上的点(0,6)时,求此时D点的坐标;

 和点
和点 在抛物线
在抛物线 上.
上. 
 的值及点
的值及点 的坐标;
的坐标;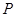 在
在 轴上,且满足△
轴上,且满足△ 是以
是以 为直角边的直角三角形,求点
为直角边的直角三角形,求点 ,点B的对应点为
,点B的对应点为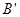 . 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,
. 点M(2,0)在x轴上,当抛物线向右平移到某个位置时, 最短,求此时抛物线的函数解析式.
最短,求此时抛物线的函数解析式.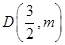 是抛物线上的一点,求△ABD的面积.
是抛物线上的一点,求△ABD的面积. 的图像经过原点及点A(1,2),与x轴相交于另一点B.
的图像经过原点及点A(1,2),与x轴相交于另一点B.
 的解析式及B点坐标;
的解析式及B点坐标; 为对称轴向右翻折后,得到一个新的二次函数
为对称轴向右翻折后,得到一个新的二次函数 ,已知二次函数
,已知二次函数