题目内容
今年,在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.(售价不低于进价).请根据小丽提供的信息,解答小华和小明提出的问题.
认真阅读上面三位同学的对话,请根据小丽提供的信息.
(1)解答小华的问题;
(2)解答小明的问题.
(1)当定价为4元时,能实现每天800元的销售利润;
(2)800元不是最大利润,当售价为每个4.8元时,利润最大为896元.
解析试题分析:(1)设定价为x元,利润为y元,根据利润=(定价﹣进价)×销售量,列出函数关系式,结合x的取值范围,求出当y取800时,定价x的值即可;
(2)根据(1)中求出的函数解析式,运用配方法求最大值,并求此时x的值即可.
试题解析:(1)设定价为x元,根据题意得:
(x-2)(500- )=800
)=800
解得x1=4 x2=6
∵售价不能超过进价的240%
∴x≤2×240% 即x≤4.8
∴x=4;
答:当定价为4元时,能实现每天800元的销售利润.
(2)设利润为y元
则y=(x-2)(500- )
)
=-10(x-5)2+900
由(1)知:2≤x≤4.8
由二次函数的性质知,当2≤x≤4.8时,y随x的增大而增大
∴当x=4.8时,y最大=896元
答:800元不是最大利润,当售价为每个4.8元时,利润最大为896元.
考点:二次函数的应用.

已知抛物线 与
与 轴相交于
轴相交于 ,
, 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴相交于点
轴相交于点 .
.
(1)点 的坐标为 ,点
的坐标为 ,点 的坐标为 ;
的坐标为 ;
(2)在 轴的正半轴上是否存在点
轴的正半轴上是否存在点 ,使以点
,使以点 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出点
相似?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
某工厂生产某品牌的护眼灯,并将护眼灯按质量分成15个等级(等级越高,质量越好.如:二级产品好于一级产品).若出售这批护眼灯,一级产品每台可获利21元,每提高一个等级每台可多获利润1元,工厂每天只能生产同一个等级的护眼灯,每个等级每天生产的台数如下表表示:
| 等级(x级) | 一级 | 二级 | 三级 | … |
| 生产量(y台/天) | 78 | 76 | 74 | … |
(2)每台护眼灯可获利z(元)关于等级x(级)的函数关系式:______;
(3)若工厂将当日所生产的护眼灯全部售出,工厂应生产哪一等级的护眼灯,才能获得最大利润?最大利润是多少?


 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
 的两个根.
的两个根.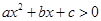 的解集.
的解集. 随
随 的增大而减小的自变量
的增大而减小的自变量 有两个不相等的实数根,求
有两个不相等的实数根,求 的取值范围.
的取值范围. .
.
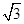 )为圆心,以2为半径的圆与
)为圆心,以2为半径的圆与 轴交于A、B两点.
轴交于A、B两点.
 的图象经过点A、B,试确定此二次函数的解析式.
的图象经过点A、B,试确定此二次函数的解析式. 经过(0,-1),(3,2)两点.求它的解析式及顶点坐标.
经过(0,-1),(3,2)两点.求它的解析式及顶点坐标.