��Ŀ����
һ�һ�����ԭ��ÿ������Ϊ120��Ԫ���ӽ���1����װʹ�û��վ����豸(��װʱ�䲻��)��һ��������˻�������һ������ԭ�ϳɱ����ݲ��㣬ʹ�û��վ����豸���1��x��(1��x��12)���������ƽ��ֵw(��Ԫ)����w��10x��90���ڶ�����������ȶ��ڵ�1��ĵ�12���µ�ˮƽ��
(1)��ʹ�û��վ����豸���1��x��(1��x��12)�������Ϊy��д��y����x�ĺ�����ϵʽ������ǰ�����µ�����͵���700��Ԫ��
(2)��xΪ��ֵʱ��ʹ�û��վ����豸���1��x�µ�������벻��װ���վ����豸ʱx���µ��������ȣ�
(3)��ʹ�û��վ����豸������������ܺͣ�
��1��5���£���2��3����3��6360��Ԫ��
���������������1����Ϊʹ�û��վ����豸���1��x�£�1��x��12�����������ƽ��ֵw����Ԫ������w=10x��90������y=xw=x��10x��90����Ҫ��ǰ�����µ������=700��Ԫ������y=700�����÷��̼��ɽ�����⣻��2����Ϊԭ��ÿ������Ϊ120��Ԫ��ʹ�û��վ����豸���1��x�µ�������벻��װ���վ����豸ʱx���µ��������ȣ�������y=120x����֮��������𰸣���3����Ϊʹ�û��վ����豸���һ�����������=12����10��12+90����������ǵĺͼ��ɣ�
����������⣺(1)y��xw��x(10x��90)��10x2��90x��
10x2��90x��700��
��ã�x��5��14(�������⣬��ȥ)��
��ǰ5���µ�����͵���700��Ԫ��
(2)10x2��90x��120x��
��ã�x��3��0(�������⣬��ȥ)��
�𣺵�xΪ3ʱ��ʹ�û��վ����豸���1��x�µ�������벻��װ���վ����豸ʱx���µ��������ȣ�
(3)��һ��ȫ��������ǣ�12(10��12��90)��2520(��Ԫ)��
ǰ11���µ��������ǣ�11(10��11��90)��2200(��Ԫ)��
���12�µ�������2520��2200��320��Ԫ��
�ڶ���������ܺ���12��320��3840��Ԫ��
2520��3840��6360(��Ԫ)��
��ʹ�û��վ����豸������������ܺ���6360��Ԫ��
���㣺һԪ���η��̵�Ӧ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д����κ���y=x2+bx+c��ͼ���㣨4,3��,��3,0����
��1��b= ,c= ��
��2��ѡȡ�ʵ���������д�±�,������ͼ��ֱ������ϵ�л����ú�����ͼ��
| x | �� | | | | | | �� |
| y | �� | | | | | | �� |
��3��������ͼ����x������ƽ��3����λ,ֱ��д��ƽ�ƺ�ͼ������Ӧ�ĺ�����ϵʽ .

 .
. ��
�� ���ཻ��
���ཻ�� ��
�� ���㣨��
���㣨�� ���ཻ�ڵ�
���ཻ�ڵ� ��
��
 ��ʹ�Ե�
��ʹ�Ե� ��
�� ���ƣ������ڣ������
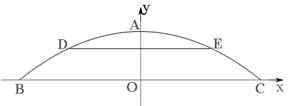
���ƣ������ڣ������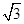 ��ΪԲ�ģ���2Ϊ�뾶��Բ��
��ΪԲ�ģ���2Ϊ�뾶��Բ�� �ύ��A��B���㣮
�ύ��A��B���㣮
 ��ͼ����A��B����ȷ���˶��κ����Ľ���ʽ��
��ͼ����A��B����ȷ���˶��κ����Ľ���ʽ�� ������0,-1��,��3,2�����㣮�����Ľ���ʽ���������꣮
������0,-1��,��3,2�����㣮�����Ľ���ʽ���������꣮
 ��ȡֵ��Χ��
��ȡֵ��Χ�� ��
�� �ύ�ڵ�A(��1��0)��B(3��0)����
�ύ�ڵ�A(��1��0)��B(3��0)���� �ύ�ڵ�C(0��3)��
�ύ�ڵ�C(0��3)��