题目内容
【题目】如图,正方形ABCD的边长为2,点E、F分别是CD、BC的中点,AE与DF交于点P,连接CP,则CP=_____.

【答案】![]()
【解析】
由△ADE≌△DCF可导出四边形CEPF对角互补,而CE=CF,于是将△CEP绕C点逆时针旋转90°至△CFG,可得△CPG是等腰直角三角形,从而PG=PF+FG=PF+PE=![]() CP,求出PE和PF的长度即可求出PC的长度.
CP,求出PE和PF的长度即可求出PC的长度.
解:如图,作CG⊥CP交DF的延长线于G.
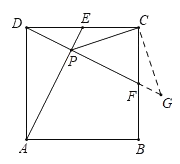
则∠PCF+∠GCF=∠PCG=90°,
∵四边形ABCD是边长为2的正方形,
∴AD=CD=BC=AB=2,∠ADC=∠DCB=90°,
∵E、F分别为CD、BC中点,
∴DE=CE=CF=BF=1,
∴AE=DF=![]() ,
,
∴DP=![]() =
=![]() ,
,
∴PE=![]() ,PF=
,PF=![]() ,
,
在△ADE和△DCF中:
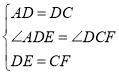
∴△ADE≌△DCF(SAS),
∴∠AED=∠DFC,
∴∠CEP=∠CFG,
∵∠ECP+∠PCF=∠DCB=90°,
∴∠ECP=∠FCG,
在△ECP和△FCG中:

∴△ECP≌△FCG(ASA),
∴CP=CG,EP=FG,
∴△PCG为等腰直角三角形,
∴PG=PF+FG=PF+PE=![]() =
=![]() CP,
CP,
∴CP=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某文具店准备购进A、B两种型号的书包共50个进行销售,两种书包的进价、售价如下表所示:
书包型号 | 进价(元/个) | 售价(元/个) |
A型 | 200 | 300 |
B型 | 100 | 150 |
购进这50个书包的总费用不超过7300元,且购进B型书包的个数不大于A型书包个数的![]() .
.
(1)该文具店有哪几种进货方案?
(2)若该文具店购进的50个书包全部售完,则该文具店采用哪种进货方案,才能获得最大利润?最大利润是多少?(利润=售价﹣进价)





