题目内容
【题目】如图，点C为线段AB的中点，E为直线AB上方的一点，且满足CE=CB，连接AE，以AE为腰，A为顶角顶点作等腰Rt△ADE，连接CD，当CD最大时，∠DEC的度数为（ ）
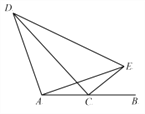
A. 60° B. 75° C. 90° D. 67.5°
【答案】D
【解析】由题意知，当CD⊥CE时，CD取得最大值，此时A、C、E、D共圆，由AC=CE可得∠ADC=∠CDE，从而可求出∠CDE的度数，再根据直角三角形两直角互余求出∠DEC的度数.
：由题意知，当CD⊥CE时，CD取得最大值，此时A、C、E、D共圆.
∵点C为线段AB的中点，
∴AC=BC.
∵CE=CB，
∴AC=CE，
∴∠ADC=∠CDE，
∵∠ADE=45，
∴∠DEC=45÷2=22.5，
∴∠DEC=90-22.5=67.5.
故选D.
练习册系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
高效智能课时作业系列答案
相关题目
