题目内容
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() 、
、![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
![]() 求该函数的表达式;
求该函数的表达式;
![]() 点
点![]() 为该函数在第一象限内的图象上一点,过点
为该函数在第一象限内的图象上一点,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() .
.
①求线段![]() 的最大值;
的最大值;
②若以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.

【答案】![]()
![]() ;
;![]() 满足条件的
满足条件的![]() 点坐标为
点坐标为![]() 或
或![]() .
.
【解析】
(1)根据待定系数法求函数关系式;(2)根据相似三角形列出比例式表示PQ值.
![]() 抛物线解析式为
抛物线解析式为![]() ,
,
即![]() ,
,
则![]() ,解得
,解得![]() ,
,
所以抛物线解析式为![]() ;
;
![]() ①作
①作![]() 轴于
轴于![]() ,交
,交![]() 于
于![]() ,如图,
,如图,
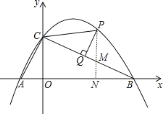
![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() ,
,![]() 得
得![]() ,解得
,解得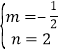 ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴当![]() 时,线段
时,线段![]() 的最大值为
的最大值为![]() ;
;
②当![]() 时,
时,![]() ,
,
此时![]() ,点
,点![]() 和点
和点![]() 关于直线
关于直线![]() 对称,
对称,
∴此时![]() 点坐标为
点坐标为![]() ;
;
当![]() 时,
时,![]() ,
,
∵![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() 为等腰三角形,
为等腰三角形,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
此时![]() 点坐标为
点坐标为![]() ,
,
综上所述,满足条件的![]() 点坐标为
点坐标为![]() 或
或![]() .
.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目