题目内容
【题目】如图,已知O为坐标原点,四边形OABC为长方形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动.
(1)当△ODP是等腰三角形时,请直接写出点P的坐标;
(2)求△ODP周长的最小值.(要有适当的图形和说明过程)

【答案】P 的坐标为:(2.5,4)或(3,4)或(2,4)或(8 ,4);(2) △ODP周长=5+![]()
【解析】试题分析:(1)当P1O=OD=5或P2O=P2D或P3D=OD=5或P4D=OD=5时,分别作P2E⊥OA于E,DF⊥BC于F,P4G⊥OA于G,利用勾股定理P1C,OE,P3F,DG的值,就可以求出P的坐标;(2)作点D关于BC的对称点D′,连接OD′交BC于P,则这时的△POD的周长最小,即△POD的周长=OD′+OD,根据勾股定理得到OD′的长 ,即可求得△POD的周长.
试题解析:
(1))当P1O=OD=5时,由勾股定理可以求得P1C=3,
当P2O=P2D时,作P2E⊥OA,∴OE=ED=2.5;
当P3D=OD=5时,作DF⊥BC,由勾股定理,得P3F=3,∴P3C=2;
当P4D=OD=5时,作P4G⊥OA,由勾股定理,得DG=3,∴OG=8.
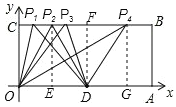
∴P1(2,4),P2(2.5,4),P3(3,4),P4(8,4);
(2) 作点D关于BC的对称点D′,连接OD′交BC于P,
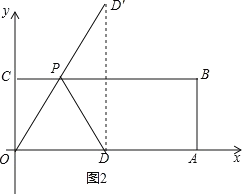
则这时的△POD的周长最小,此时△POD的周长=OD′+OD,
∵点D是OA的中点,
∴OD=5,DD′=8,
∴OD′=![]() ,
,
∴△POD的周长=![]() +5.
+5.

练习册系列答案
相关题目