Question

【题目】如图，已知反比例函数和一次函数y=2x﹣1，其中一次函数的图象经过（a，b），（a+1，b+k）两点．

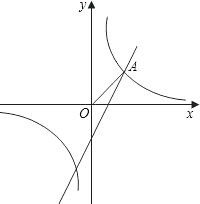
（1）求反比例函数的解析式；

（2）如图，已知点A在第一象限，且同时在上述两个函数的图象上，求点A的坐标；

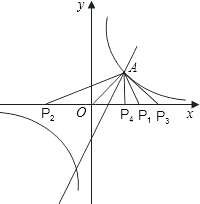
（3）利用（2）的结果，请问：在x轴上是否存在点P，使△AOP为等腰三角形？若存在，把符合条件的P点坐标都求出来；若不存在，请说明理由．

Answer 1

【答案】（1）y=．（2）点A的坐标为（1，1）；（3）符合条件的点有4个，分别是（，0），（﹣，0），（2，0），（1，0）．

【解析】

试题分析：（1）把过一次函数的两个点代入一次函数，即可求得k，进而求得反比例函数的解析式．

（2）同时在这两个函数解析式上，让这两个函数组成方程组求解即可．

（3）应先求出OA的距离，然后根据：OA=OP，OA=AP，OP=AP，分情况讨论解决．

解：（1）由题意得

②﹣①得k=2

∴反比例函数的解析式为y=．

（2）由，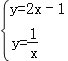

解得，．

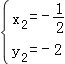∵点A在第一象限，

∴点A的坐标为（1，1）

（3），OA与x轴所夹锐角为45°，

①当OA为腰时，由OA=OP1得P1（，0），

由OA=OP2得P2（﹣，0）；

由OA=AP3得P3（2，0）．

②当OA为底时，OP4=AP4得P4（1，0）．

∴符合条件的点有4个，分别是（，0），（﹣，0），（2，0），（1，0）．