题目内容
【题目】甲布袋中有三个红球，分别标有数字1，2，3；乙布袋中有三个白球，分别标有数字2，3，4．这些球除颜色和数字外完全相同．小亮从甲袋中随机摸出一个红球，小刚从乙袋中随机摸出一个白球．
（1）用画树状图（树形图）或列表的方法，求摸出的两个球上的数字之和为6的概率；
（2）小亮和小刚做游戏，规则是：若摸出的两个球上的数字之和为奇数，小亮胜；否则，小刚胜．你认为这个游戏公平吗？为什么？
【答案】（1）见解析；
．（2）这个游戏不公平，见解析
【解析】
试题分析：游戏是否公平，关键要看游戏双方获胜的机会是否相等，即判断双方取胜的概率是否相等，或转化为在总情况明确的情况下，判断双方取胜所包含的情况数目是否相等．
解：
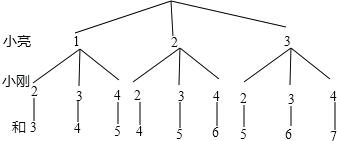
（1）解法一：树状图
（3分）
∴P（两个球上的数字之和为6）=．（2分）
解法二：列表
2 | 3 | 4 | |
1 | （1，2） | （1，3） | （1，4） |
2 | （2，2） | （2，3） | （2，4） |
3 | （3，2） | （3，3） | （3，4） |
∴P（两个球上的数字之和为6）=．
（2）不公平．（1分）
∵P（小亮胜）=
，P（小刚胜）=
．（2分）
∴P（小亮胜）≠P（小刚胜）．
∴这个游戏不公平．（2分）
练习册系列答案
相关题目
