Question

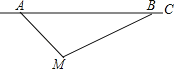
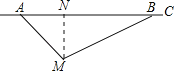
【题目】根据道路管理规定，在贺州某段笔直公路上行驶的车辆，限速40千米/时，已知交警测速点M到该公路A点的距离为10米，∠MAB=45°，∠MBA=30°（如图所示），现有一辆汽车由A往B方向匀速行驶，测得此车从A点行驶到B点所用的时间为3秒．

（1）求测速点M到该公路的距离；

（2）通过计算判断此车是否超速．（参考数据：≈1.41，≈1.73，≈2.24）

Answer 1

【答案】（1）10米；（2）此车没有超速．

【解析】

试题分析：（1）过M作MN垂直于AB，在直角三角形AMN中，利用锐角三角函数定义及特殊角的三角函数值求出MN的长，即可得到结果；

（2）由三角形AMN为等腰直角三角形得到AN=MN=10米，在直角三角形BMN中，利用锐角三角函数定义求出BN的长，由AN+NB求出AB的长，根据路程除以时间得到速度，即可做出判断．

解：（1）过M作MN⊥AB，

在Rt△AMN中，AM=10，∠MAN=45°，

∴sin∠MAN=，即=，

解得：MN=10，

则测速点M到该公路的距离为10米；

（2）由（1）知：AN=MN=10米，

在Rt△MNB中，∠MBN=30°，

由tan∠MBN=，得：=，

解得：BN=10（米），

∴AB=AN+NB=10+10≈27.3（米），

∴汽车从A到B的平均速度为27.3÷3=9.1（米/秒），

∵9.1米/秒=32.76千米/时＜40千米/时，

∴此车没有超速．