题目内容
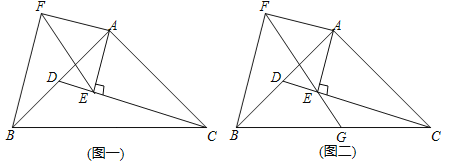
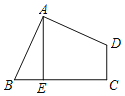
【题目】如图，在四边形ABCD中，∠BAD＝∠C＝90°，AB＝AD，AE⊥BC于E点，AE＝2，则四边形ABCD的面积为（ ）
A.2B.3C.4D.6
【答案】C
【解析】
过点A作AF⊥AE，交CD的延长线于点F，由题意可证△ABE≌△ADF，可得AE＝AF，则可证四边形AECF是正方形，四边形ABCD的面积即为正方形AECF的面积．
解：过点A作AF⊥AE，交CD的延长线于点F
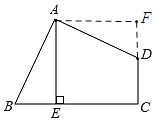
∵∠BAD＝∠C＝90°，AE⊥BC，AE⊥AF
∴四边形AECF是矩形
∴∠F＝90°
∵AE⊥AF，BA⊥AD
∴∠BAE+∠DAE＝90°，∠DAF+∠DAE＝90°
∴∠BAE＝∠DAE
又∵AB＝AD，∠F＝∠AEB＝90°
∴△ADF≌△ABE（AAS）
∴AF＝AE，S△ADF＝S△ABE．
∴四边形AECF是正方形．
∴S正方形AECF＝AE2＝4
∵S四边形ABCD＝S△ABE+S四边形AECD＝S△ADF+S四边形AECD．
∴S四边形ABCD＝S正方形AECF＝4
故选：C．
练习册系列答案
名校课堂系列答案
相关题目
【题目】已知二次函数y＝ax2＋bx＋c（a≠0）图象上部分点的坐标（x，y）的对应值如下表所示：
x | … | 0 |
| 4 | … |
y | … | 0.37 | -1 | 0.37 | … |
则方程ax2＋bx＋1.37＝0的根是（ ）
A.0或4B.
或
C.1或5D.无实根
