题目内容
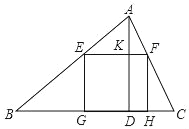
【题目】如图,一块材料的形状是锐角三角形ABC,边BC长120mm,高AD为80mm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)图中与△ABC相似的三角形是哪一个,说明理由;
(2)这个正方形零件的边长为多少?
【答案】(1)△AEF;(2)正方形零件的边长为48mm.
【解析】
(1)根据矩形的对边平行得到BC∥EF,利用“平行于三角形的一边的直线截其他两边或其他两边的延长线,得到的三角形与原三角形相似”判定即可.
(2)设正方形零件的边长为x mm,则KD=EF=x,AK=80-x,根据EF∥BC,得到△AEF∽△ABC,根据相似三角形的性质得到比例式,解方程即可得到结果.
(1)∵正方形EGHF,
∴EF∥BC,
∴△AEF∽△ABC,
故答案为:△AEF;
(2)设EG=EF=x
∵△AEF∽△ABC
∴![]() ,
,
∴![]() ,
,
∴x=48,
∴正方形零件的边长为48mm.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目