��Ŀ����
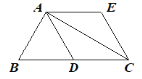
����Ŀ����ͼ����֪ B 1, 0 �� C 1, 0 �� A Ϊ y ����������һ�㣬 AB AC ���� D Ϊ�ڶ�����һ���㣬E �� BD ���ӳ����ϣ� CD �� AB �� F ����BDC BAC .
��1����֤�� ABD ACD ��
��2����֤�� AD ƽ��CDE ��
��3������ D ���˶��Ĺ����У�ʼ���� DC DA DB ���ڴ˹����У�BAC �Ķ����Ƿ�仯������仯����˵�����ɣ�������䣬�����BAC �Ķ�����
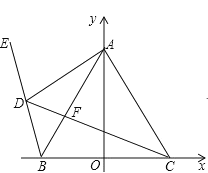
���𰸡���1������������2������������3����BAC�Ķ������仯����BAC=60����
��������
��1�������������ڽǺͶ������������ɵý��ۣ���2����AM��CD�ڵ�M����AN��BE�ڵ�N��֤����ACM�ա�ABN���ɣ���3���ýس����̷���CD�Ͻ�ȡCP=BD������AP��֤����ABD�ա�ACP����ȫ�����ʿ�֪��ADP�ǵȱ������Σ���֪BAC �Ķ���.
��1���ߡ�BDC=��BAC����DFB=��AFC��
�֡ߡ�ABD+��BDC+��DFB=��BAC+��ACD+��AFC=180����
���ABD=��ACD��
��2������A��AM��CD�ڵ�M����AN��BE�ڵ�N��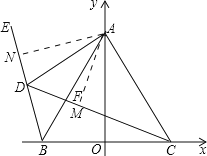
���AMC=��ANB=90����
��OB=OC��OA��BC��
��AB=AC��
�ߡ�ABD=��ACD��
���ACM�ա�ABN ��AAS��
��AM=AN��
��ADƽ�֡�CDE�������ǵ����߾�����ȵĵ��ڽǵ�ƽ�����ϣ���
��3����BAC�Ķ������仯��
��CD�Ͻ�ȡCP=BD������AP��
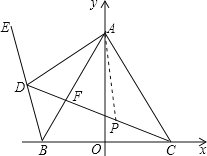
��CD=AD+BD��
��AD=PD��
��AB=AC����ABD=��ACD��BD=CP��
���ABD�ա�ACP��
��AD=AP����BAD=��CAP��
��AD=AP=PD������ADP�ǵȱ������Σ�
���DAP=60����
���BAC=��BAP+��CAP=��BAP+��BAD=60����

����Ŀ������ڼ䣬С��ͬѧ�ڹ���ѧ����һ����Ȫˮ���˶��������˶����������ۣ���������ۼ����±���
���ۣ�Ԫ/ƿ�� | �ۼۣ�Ԫ/ƿ�� | |
��Ȫˮ | 0.75 | 2 |
�˶����� | 3 | 4 |
��1����С��ͬѧ������Ȫˮ���˶����Ϲ� 30 ƿ����ȥ�� 67.5 Ԫ������ȫ�����꣬��С��ͬѧ�ڸ��������˶���Ǯ��
��2��Ϊ�˽�һ������ͬѧ�ǵ�����С��ͬѧ�����ò����� 400 Ԫ���ʽ���Ȫˮ���˶����Ϲ�200 ƿ������������ƿ�˶����ϣ�
��3��С��ͬѧǮ��Ϊ�˻ر���ᣬ����һ���鼮��ƶ��ɽ���ĺ��ӣ�����ָ�ÿλ���� 4 ���飬��ôʣ�� 10 ���飻����ָ�ÿλ���� 5 ���飬��ô���һλ���ӷֵõ��鲻�� 4 ����������1������С��ͬѧ���˶��ٱ��飿