题目内容
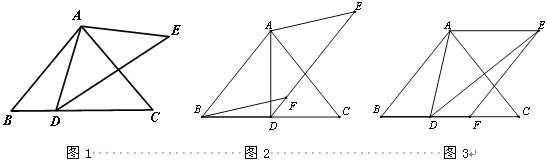
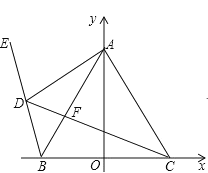
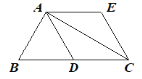
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的中线,
边上的中线,![]() ∥
∥![]() ,且
,且![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)连接![]() ,若
,若![]() 平分
平分![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]()
【解析】(1)由中线的定义和已知可得到AE=CD,再根据一组对边平行且相等的四边形是平行四边形得到四边形ADCE为平行四边形,由∠BAC=90°,AD为BC边上的中线,得到AD=![]() BC=CD.即可得到四边形ADCE为菱形.
BC=CD.即可得到四边形ADCE为菱形.
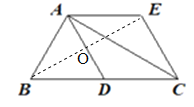
(2)连接BE与AD相交于点O.由角平分线的性质和平行线的性质可得到AB=AE,由BD=![]() BC=AE,得到AB=BD,由等腰三角形三线合一的性质得到∠BOD=90°.由AD∥CE,得到∠BEC=∠BOD=90°.在△BEC中,由勾股定理即可得出结论.
BC=AE,得到AB=BD,由等腰三角形三线合一的性质得到∠BOD=90°.由AD∥CE,得到∠BEC=∠BOD=90°.在△BEC中,由勾股定理即可得出结论.
(1)∵AD为BC边上的中线,∴BD=CD=![]() BC.
BC.
∵AE=![]() BC,∴AE=CD.
BC,∴AE=CD.
∵AE∥BC,∴四边形ADCE为平行四边形(一组对边平行且相等的四边形是平行四边形).
∵∠BAC=90°,AD为BC边上的中线,∴AD=![]() BC=CD,
BC=CD,
∴四边形ADCE为菱形(有一组邻边相等的平行四边形是菱形)
(2)连接BE与AD相交于点O.
∵若BE平分∠ABC,∴∠ABE=∠CBE .
∵AE∥BC,∴∠AEB=∠CBE,∴∠ABE=∠AEB,∴AB=AE.
∵BD=![]() BC=AE,∴AB=BD,∴∠BOD=90°.
BC=AE,∴AB=BD,∴∠BOD=90°.
∵四边形ADCE为菱形,AE=2,∴AD=DC=CE=AE=2,BC=4.
∵AD∥CE,∴∠BEC=∠BOD=90°,∴![]() .
.

【题目】A、B两店分另选5名销售员某月的销售额(单位:万元)进行分析,数据如下图表(不完整):
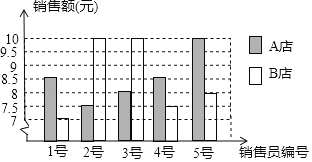
平均数 | 中位数 | 众数 | |
A店 | 8.5 |
|
|
B店 |
| 8 | 10 |
(1)根据图a数据填充表格b所缺的数据;
(2)如果A店想让一半以上的销售员达到销售目标,你认为月销售额定为多少合适?说明理由.