题目内容
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,现将矩形
,现将矩形![]() 折叠使点
折叠使点![]() 与点
与点![]() 重合,则折痕
重合,则折痕![]() 的长是( )
的长是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
设BE=x,表示出CE=8-x,根据翻折的性质可得AE=CE,然后在Rt△ABE中,利用勾股定理列出方程求出x,再根据翻折的性质可得∠AEF=∠CEF,根据两直线平行,内错角相等可得∠AFE=∠CEF,然后求出∠AEF=∠AFE,根据等角对等边可得AE=AF,过点E作EH⊥AD于H,可得四边形ABEH是矩形,根据矩形的性质求出EH、AH,然后求出FH,再利用勾股定理列式计算即可得解.
设BE=x,则CE=BC-BE=8-x,
∵沿EF翻折后点C与点A重合,
∴AE=CE=8-x,
在Rt△ABE中,AB2+BE2=AE2,
即42+x2=(8-x)2
解得x=3,
∴AE=8-3=5,
由翻折的性质得,∠AEF=∠CEF,
∵矩形ABCD的对边AD∥BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AE=AF=5,
过点E作EH⊥AD于H,则四边形ABEH是矩形,
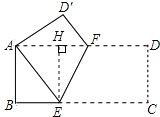
∴EH=AB=4,
AH=BE=3,
∴FH=AF-AH=5-3=2,
在Rt△EFH中,EF=![]() =
=![]() .
.
故选A.

练习册系列答案
相关题目
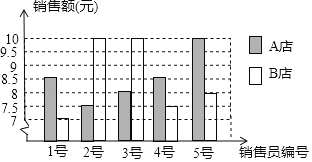
【题目】A、B两店分另选5名销售员某月的销售额(单位:万元)进行分析,数据如下图表(不完整):
平均数 | 中位数 | 众数 | |
A店 | 8.5 |
|
|
B店 |
| 8 | 10 |
(1)根据图a数据填充表格b所缺的数据;
(2)如果A店想让一半以上的销售员达到销售目标,你认为月销售额定为多少合适?说明理由.