题目内容
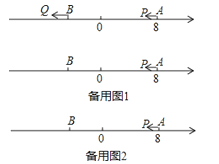
【题目】如图,请按照要求回答问题:![]()
(1) 数轴上的点C表示的数是 线段AB的中点D表示的数是 ﹣2 ;
(2)线段AB的中点D与线段BC的中点E的距离DE等于多少?
(3)在数轴上方有一点M,下方有一点N,且∠ABM=120°,∠CBN=60°,请画出示意图,判断BC能否平分∠MBN,并说明理由.
【答案】
(1)2.5;-2
(2)
解:∵线段BC的中点E表示的数是![]() =0.75,
=0.75,
∴DE=|﹣2﹣0.75|=2.75;
(3)
解:如下图(可以不标出角的度数):
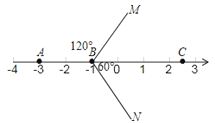
BC平分∠MBN.理由是:
∵∠ABM=120°,
∴∠MBC=180°﹣120°=60°,
又∠CBN=60°,
∴∠MBC=∠CBN,
即BC平分∠MBN.
【解析】(1)观察数轴,即可知道点C表示的数;根据线段中点表示的数=这条线段的两个端点表示的数的和÷2作答;
(2)首先求出点E表示的数,然后根据数轴上两点之间的距离等于它们所表示的数的差的绝对值,即可得出DE的长;
(3)首先画出图形,然后计算出∠MBC的度数,再与∠CBN比较即可.
【考点精析】本题主要考查了线段长短的计量和角的平分线的相关知识点,需要掌握度量法:即用一把刻度量出两条线段的长度再比较;叠合法:从“形”的角度比较,观察点的位置;从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目