题目内容
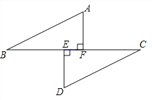
【题目】(1)问题发现,如图1,在正方形ABCD中,点E为CD的中点,过点D作AE的垂线,垂足为F与AC、BC分别交于点G,点H,则![]() = .
= .
(2)类比探究;如图2,在矩形ABCD中,![]() ,点E为CD的中点,过点D作AE的垂线,垂足为F,与AC、BC分别交于点G,点H,试探究
,点E为CD的中点,过点D作AE的垂线,垂足为F,与AC、BC分别交于点G,点H,试探究![]() 的值,并写出推理过程.
的值,并写出推理过程.

【答案】(1)2;(2)![]() ,理由详见解析.
,理由详见解析.
【解析】
试题分析:(1)根据正方形性质证明△ADE≌△DCH,得CH=DE,设DE=x,根据AD∥CH得比例式得结论;
(2)设AD=3x,DC=4x,证明△ADE∽△DCH,表示出CH的长,利用AD∥BC列比例式代入求解.
试题解析:(1)如图1,设DE=x,则DC=2x,AD=2x,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∵DC=AD,∠ADC=∠DCH=90°,
∴△ADE≌△DCH,
∴CH=DE=x,
∵AD∥CH,
∴△ADG∽△CHG,
∴![]() =2.
=2.
故答案为:2;
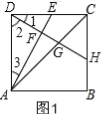
(2)如图2,设AD=3x,DC=4x,则DE=2x,
∵∠HDC+∠ADH=90°,∠ADH+∠DAE=90°,
∴∠HDC=∠DAE,
∵∠ADC=∠DCB=90°,
∴△ADE∽△DCH,
∴![]() ,
,
∴![]() ,
,
∴CH=![]() ,
,
∵AD∥BC,
∴△ADG∽△CHG,
∴![]() =
=![]() =
=![]() .
.

【题目】某手机专卖店销售A,B两种型号的手机,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售利润 | |
A型 | B型 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3000元 |
(1)求每台A型手机和B型手机的销售利润;
(2)该手机专卖店计划一次购进两种型号的手机共100台,其中A型号手机的进货量不超过B型号手机进货量的2倍.设购进A型号手机x台,这100台手机的销售总利润为y元.
①求y关于x的函数表达式;
②该商店购进A型号和B型号手机各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型号手机的出厂价提高a(0<a<100)元,对B型号手机的出厂价下降a(0<a<100)元,且限定该手机专卖店至少购进A型号手机20台.若该手机专卖店保持两种手机的售价不变,请根据以上信息及(2)中条件,设计出使这100台手机销售总利润最大的进货方案.