��Ŀ����
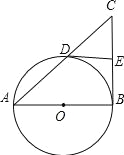
����Ŀ����ͼ����֪�����ϵ�A��B�������ϵ�һ�㣬AB=12������P�ӵ�A��������ÿ��6����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮
��1��д�������ϵ�B��ʾ��������t����P�߹���·��Ϊ���ú�t�Ĵ���ʽ��ʾ����
��2�����ڶ���P�˶���ͬʱ��һ����Q�ӵ�BҲ����������ÿ��4����λ���ȵ��ٶ����������������˶����ʾ�����ʱ���P�����ϵ�Q��
��3����MΪAP���е㣬NΪBP���е㣬��P���˶��Ĺ����У��߶�MN�ij����Ƿ����仯�����仯����˵�����ɣ������䣬���㻭��ͼ�Σ�������߶�MN�ij���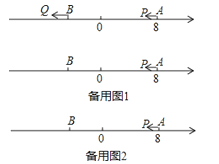
���𰸡��⣺��1����B���ʾx������
AB=8��x=12�����x=��4��
�߶���P�ӵ�A��������ÿ��6����λ���ȵ��ٶ����������������˶���
�ྭt����P�߹���·��Ϊ6t��
�ʴ�Ϊ����4��6t��
��2���辭t���P����Q�㣬��������ã�
6t��4t=12��
���t=6��
�𣺾���6��ʱ���P�����ϵ�Q��
��3������P���˶�������߶�MN������6��
���������������
�ٵ�P���߶�AB��ʱ����ͼ1��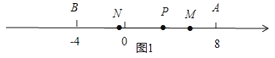
MN=PM+PN=![]() PA+
PA+![]() PB=
PB=![]() ��PA+PB��=
��PA+PB��=![]() AB=
AB=![]() ��12=6��
��12=6��
�ڵ�P���߶�AB���ӳ�����ʱ����ͼ2��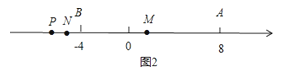
MN=PM��PN=![]() PA��
PA��![]() PB=
PB=![]() ��PA��PB��=
��PA��PB��=![]() AB=
AB=![]() ��12=6��
��12=6��
���Ͽ�֪������P�˶�������߶�MN�ij��ȶ����䣬������6��
����������1�����B���ʾ����Ϊx���������������ľ��뼴�ɵõ�x�ķ��̣��ⷽ�̼��ɵó�x����·��=�ٶȡ�ʱ��ɵó���P�߹���·�̣�
��2���辭t���P����Q�㣬��������ɵã�����t��һԪһ�η��̣��ⷽ�̼��ɵó�ʱ��t��
��3����P��λ�õIJ�ͬ������������ǣ������е�Ķ��壬�����ҵ��߶μ�Ĺ�ϵ���Ӷ����ҳ�MN�ij��ȣ�
�����㾫�����������⣬������Ҫ�˽�����(�����ǹ涨��ԭ�㡢������λ���ȵ�һ��ֱ��)��

����Ŀ��ijУ���������10����Ա���ж���Ͷ����ϰ��ÿ��Ͷ��10�Σ�����Ͷ�еĴ���ͳ�������
Ͷ�д��� | 3 | 5 | 6 | 7 | 8 |
���� | 1 | 3 | 2 | 2 | 2 |
����Щ��ԱͶ�д���������Ϊ___________��
����Ŀ��ij�ֻ�ר��������A��B�����ͺŵ��ֻ�������ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A�� | B�� | ||
��һ�� | 3̨ | 5̨ | 1800Ԫ |
�ڶ��� | 4̨ | 10̨ | 3000Ԫ |
��1����ÿ̨A���ֻ���B���ֻ�����������
��2�����ֻ�ר����ƻ�һ�ι��������ͺŵ��ֻ���100̨������A�ͺ��ֻ��Ľ�����������B�ͺ��ֻ���������2�����蹺��A�ͺ��ֻ�x̨����100̨�ֻ�������������ΪyԪ��
����y����x�ĺ�������ʽ��
�����̵깺��A�ͺź�B�ͺ��ֻ�������̨������ʹ�������������
��3��ʵ�ʽ���ʱ�����Ҷ�A�ͺ��ֻ��ij��������a��0��a��100��Ԫ����B�ͺ��ֻ��ij������½�a��0��a��100��Ԫ���������ֻ�ר�������ٹ���A�ͺ��ֻ�20̨�������ֻ�ר���걣�������ֻ����ۼ۲��䣬�����������Ϣ����2������������Ƴ�ʹ��100̨�ֻ��������������Ľ���������