题目内容

证明：三角形的一个外角等于和它不相邻的两个内角和．

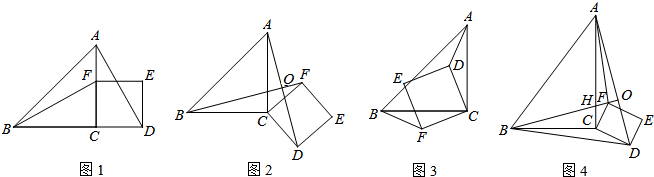
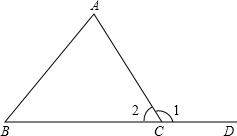
已知：如图，∠1是△ABC的一个外角，
求证：∠1=∠A+∠B，
证明：在△ABC中，∠A+∠B+∠2=180°，
∵∠1+∠2=180°，
∴∠1=∠A+∠B．
分析：写出已知、求证，然后根据三角形的内角和定理以及平角等于180°列式整理即可得证．
点评：本题主要考查了三角形外角性质的证明，是文字叙述性命题，要注意证明格式，写出已知、求证，然后写出证明推理步骤．
练习册系列答案
相关题目
如图，已知矩形ABCD，AB=
3
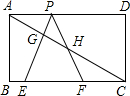，BC=3，在BC上取两点E、F（E在F左边），以EF为边作等边三角精英家教网形PEF，使顶点P在AD上，PE、PF分别交AC于点G、H．
（1）求△PEF的边长；
（2）在不添加辅助线的情况下，从图中找出一个除△PEF外的等腰三角形，并说明理由；
（3）若△PEF的边EF在线段BC上移动．试猜想：PH与BE有何数量关系？并证明你猜想的结论．
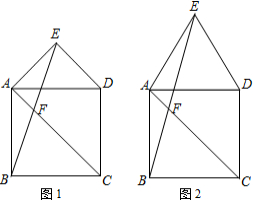精英家教网已知点E是正方形ABCD外的一点，EA=ED，线段BE与对角线AC相交于点F，
（1）如图1，当BF=EF时，线段AF与DE之间有怎样的数量关系？并证明；
（2）如图2，当△EAD为等边三角形时，写出线段AF、BF、EF之间的一个数量关系，并证明．
（2013•营口）如图1，△ABC为等腰直角三角形，∠ACB=90°，F是AC边上的一个动点（点F与A、C不重合），以CF为一边在等腰直角三角形外作正方形CDEF，连接BF、AD．
（1）①猜想图1中线段BF、AD的数量关系及所在直线的位置关系，直接写出结论；
②将图1中的正方形CDEF，绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2、图3的情形．图2中BF交AC于点H，交AD于点O，请你判断①中得到的结论是否仍然成立，并选取图2证明你的判断．
（2）将原题中的等腰直角三角形ABC改为直角三角形ABC，∠ACB=90°，正方形CDEF改为矩形CDEF，如图4，且AC=4，BC=3，CD=
43
，CF=1，BF交AC于点H，交AD于点O，连接BD、AF，求BD2+AF2的值．
（2013•金华模拟）探究：如图（1），在?ABCD的形外分别作等腰直角△ABF和等腰直角△ADE，∠FAB=∠EAD=90°，连接AC，EF．在图中找一个与△FAE全等的三角形，并加以证明．
应用：以?ABCD的四条边为边，在其形外分别作正方形，如图（2），连接EF，GH，IJ，KL．若?ABCD的面积为6，则图中阴影部分四个三角形的面积和为
12
12
．
推广：以?ABCD的四条边为矩形长边，在其形外分别作长与宽之比为
3
矩形，如图（3），连接EF，GH，IJ，KL．若图中阴影部分四个三角形的面积和为12
3
，求?ABCD的面积？
在△ABC中，AB、BC、AC三边的长分别为
5
、
10
、
13
，求这个三角形的面积．小华同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．
（1）△ABC的面积为：
3.5
3.5
．
（2）若△DEF三边的长分别为
5
、
8
、
17
，请在图2的正方形网格中画出相应的△DEF，并利用构图法求出它的面积为
3
3
．
（3）如图3，△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q．试探究EP与FQ之间的数量关系，并证明你的结论．
（4）如图4，一个六边形的花坛被分割成7个部分，其中正方形PRBA，RQDC，QPFE的面积分别为13m2、25m2、36m2，则六边形花坛ABCDEF的面积是
110
110
m2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网