题目内容
如图,已知矩形ABCD,AB=| 3 |
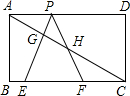 形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.(1)求△PEF的边长;
(2)在不添加辅助线的情况下,从图中找出一个除△PEF外的等腰三角形,并说明理由;
(3)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有何数量关系?并证明你猜想的结论.
分析:(1)过P作PQ垂直于BC,垂足为Q,由ABCD为矩形,得到角B为直角,且AD平行于BC,得到PQ=AB,又三角形PEF为等边三角形,根据“三线合一”得到∠FPQ为30°,在直角三角形FPQ中,设出QF为x,则PF=2x,由PQ的长,根据勾股定理列出关于x的方程,求出x的值,即可得到PF的长,即为等边三角形的边长;
(2)△APH为等腰三角形,理由是:由AB和BC,根据勾股定理求出AC的长,发现CD等于AC的一半,根据直角三角形中,一直角边等于斜边的一半,这条直角边所对的角为30°,即∠PAH为30°,又根据矩形的对边平行,得到内错角∠DPF=∠PFE=60°,又∠DPF为△APH的外角,根据外角定理得到∠PHA=30°,然后根据等角对等边得到AP=HP,故△APH为等腰三角形;
(3)PH-BE=1,理由是:过E作ER垂直于AD,如图所示,根据矩形的对边平行得到一对内错角相等,可得∠APE=60°,在直角三角形EPR中,∠REP=30°,根据直角三角形中,30°角所对的直角边等于斜边的一半,由PE求出PR,由(2)中得到PA=PH,则PH-BE=PA-BE=PA-AR=PR,即可得到两线段的关系.
(2)△APH为等腰三角形,理由是:由AB和BC,根据勾股定理求出AC的长,发现CD等于AC的一半,根据直角三角形中,一直角边等于斜边的一半,这条直角边所对的角为30°,即∠PAH为30°,又根据矩形的对边平行,得到内错角∠DPF=∠PFE=60°,又∠DPF为△APH的外角,根据外角定理得到∠PHA=30°,然后根据等角对等边得到AP=HP,故△APH为等腰三角形;
(3)PH-BE=1,理由是:过E作ER垂直于AD,如图所示,根据矩形的对边平行得到一对内错角相等,可得∠APE=60°,在直角三角形EPR中,∠REP=30°,根据直角三角形中,30°角所对的直角边等于斜边的一半,由PE求出PR,由(2)中得到PA=PH,则PH-BE=PA-BE=PA-AR=PR,即可得到两线段的关系.
解答: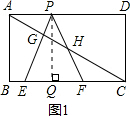 解:(1)过P作PQ⊥BC于Q(如图1)
解:(1)过P作PQ⊥BC于Q(如图1)
∵矩形ABCD,∴∠B=90°,即AB⊥BC,
又AD∥BC,∴PQ=AB=
∵△PEF是等边三角形,∴∠PFQ=60°
在Rt△PQF中,∠FPQ=30°,
设PF=2x,QF=x,PQ=
,
根据勾股定理得:(2x)2=x2+(
)2,
解得:x=1,故PF=2,
∴△PEF的边长为2.
(2)△APH是等腰三角形.理由如下:
在Rt△ADC中,AB=
,BC=3,∴由勾股定理得AC=2
,
∴CD=
AC,∴∠CAD=30°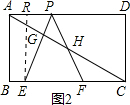
∵AD∥BC,∠PFE=60°,∴∠FPD=60°,
∴∠PHA=30°=∠CAD,∴PA=PH,
∴△APH是等腰三角形.
(3)PH-BE=1,理由如下:
作ER⊥AD于R(如图2)
Rt△PER中,∠RPE=60°,
∴PR=
PE=1,∴PH-BE=PA-BE=PR=1.
 解:(1)过P作PQ⊥BC于Q(如图1)
解:(1)过P作PQ⊥BC于Q(如图1)∵矩形ABCD,∴∠B=90°,即AB⊥BC,
又AD∥BC,∴PQ=AB=
| 3 |
∵△PEF是等边三角形,∴∠PFQ=60°
在Rt△PQF中,∠FPQ=30°,
设PF=2x,QF=x,PQ=
| 3 |
根据勾股定理得:(2x)2=x2+(
| 3 |
解得:x=1,故PF=2,
∴△PEF的边长为2.
(2)△APH是等腰三角形.理由如下:
在Rt△ADC中,AB=
| 3 |
| 3 |
∴CD=
| 1 |
| 2 |

∵AD∥BC,∠PFE=60°,∴∠FPD=60°,
∴∠PHA=30°=∠CAD,∴PA=PH,
∴△APH是等腰三角形.
(3)PH-BE=1,理由如下:
作ER⊥AD于R(如图2)
Rt△PER中,∠RPE=60°,
∴PR=
| 1 |
| 2 |
点评:此题综合考查了矩形的性质,等腰三角形的判别与性质、等边三角形的性质及直角三角形的性质.学生作第三问时,应借助第二问的结论,结合图形,多次利用数学中等量代换的方法解决问题,这就要求学生在作几何题时注意合理运用各小题之间的联系.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
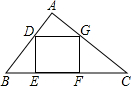 如图,已知矩形DEFG内接于Rt△ABC,D在AB上,E、F在BC上,G在AC上,∠BAC=90°,AB=6cm,AC=8cm,
如图,已知矩形DEFG内接于Rt△ABC,D在AB上,E、F在BC上,G在AC上,∠BAC=90°,AB=6cm,AC=8cm,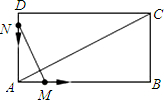 m/秒的速度移动,如果M、N两点同时出发,移动的时间为x秒(0≤x≤6).
m/秒的速度移动,如果M、N两点同时出发,移动的时间为x秒(0≤x≤6).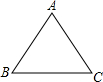 点A运动.
点A运动. (2012•宁德质检)如图,已知Rt△ABC,∠B=90°,AB=8,BC=6,把斜边AC平均分成n段,以每段为对角线作边与AB、BC平行的小矩形,则这些小矩形的面积和是( )
(2012•宁德质检)如图,已知Rt△ABC,∠B=90°,AB=8,BC=6,把斜边AC平均分成n段,以每段为对角线作边与AB、BC平行的小矩形,则这些小矩形的面积和是( )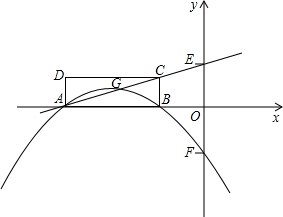 如图,已知矩形ABCD中AB:BC=3:1,点A、B在x轴上,直线y=mx+n(0<m<n<
如图,已知矩形ABCD中AB:BC=3:1,点A、B在x轴上,直线y=mx+n(0<m<n<