题目内容
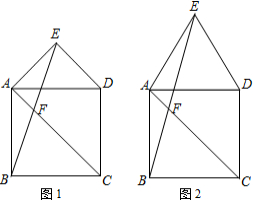 已知点E是正方形ABCD外的一点,EA=ED,线段BE与对角线AC相交于点F,
已知点E是正方形ABCD外的一点,EA=ED,线段BE与对角线AC相交于点F,(1)如图1,当BF=EF时,线段AF与DE之间有怎样的数量关系?并证明;
(2)如图2,当△EAD为等边三角形时,写出线段AF、BF、EF之间的一个数量关系,并证明.
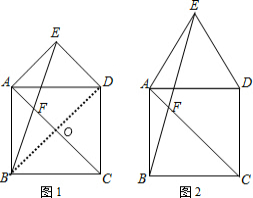
分析:(1)要求AF与DE之间有怎样的数量关系,而题目涉及在正方形中,连接正方形的对角线是常用的方法,连接对角线BD是关键,得到四边形ODEA是正方形,利用三角形中位线的性质得到结论.
(2)这个关系要用第一问类似的方法得出,辅助线不可少,制造全等三角形是难点.
(2)这个关系要用第一问类似的方法得出,辅助线不可少,制造全等三角形是难点.
解答:解:(1)AF=
DE,
证明如下:连接BD交AC于点O,
∵四边形ABCD是正方形,
∴BO=DO,
∵BF=EF,
∴OF=
DE,OF∥DE.
∵BD⊥AC,
∴∠EDO=∠AOB=90°,
∵∠ODA=∠OAD=
×90°=45°,EA=ED,
∴∠EAD=∠EDA=45°,
∴∠OAD=∠AED=∠AOD=90°,
∴四边形AODE是正方形.
∴OA=DE,
∴OF=
AO,
∴AF=
AO=
DE.
(2)AF+BF=EF、AF2+EF2=2BF2等(只要其中一个),
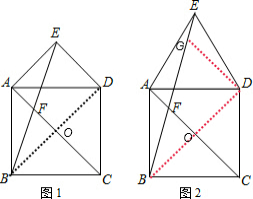
AF+BF=EF的证明方法一:
连接BD交AC于O,在FE上截取FG=BF,连接DG.
与第(1)同理可证∠GDA=45°,
∵四边形ABCD是正方形,△ADE是等边三角形,
∴∠GDE=60°-45°=15°.
∵AB=AD=AE,∠BAE=∠BAD+∠DAE=90°+60°=150°,
∴∠ABE=∠AEB=
=15°,
∴∠ABF=∠GDE.
又∵∠DEG=∠DEA-∠AEB=60°-15°=45°=∠BAC,DE=AD=AB,
∴△ABF≌△EDG
∴EG=AF,
∴AF+BF=EG+FG=EF.
AF+BF=EF的证明方法二(简略):
在FE上截取FG=AF,连接AG.证得△AFG为等边三角形.
证得△ABF≌△AEG.
证得AF+BF=EF.
AF2+EF2=2BF2的证明方法(简略):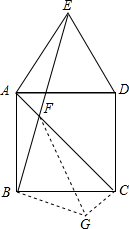
作BG⊥BF,且使BG=BF,连接CG、FG,证得△BGC≌△BFA.
证得FC=FE,FG=
BF,
利用Rt△FCG中,得出AF2+EF2=2BF2.
| 1 |
| 2 |
证明如下:连接BD交AC于点O,
∵四边形ABCD是正方形,
∴BO=DO,
∵BF=EF,
∴OF=
| 1 |
| 2 |
∵BD⊥AC,
∴∠EDO=∠AOB=90°,

∵∠ODA=∠OAD=
| 1 |
| 2 |
∴∠EAD=∠EDA=45°,
∴∠OAD=∠AED=∠AOD=90°,
∴四边形AODE是正方形.
∴OA=DE,
∴OF=
| 1 |
| 2 |
∴AF=
| 1 |
| 2 |
| 1 |
| 2 |
(2)AF+BF=EF、AF2+EF2=2BF2等(只要其中一个),
AF+BF=EF的证明方法一:
连接BD交AC于O,在FE上截取FG=BF,连接DG.
与第(1)同理可证∠GDA=45°,
∵四边形ABCD是正方形,△ADE是等边三角形,
∴∠GDE=60°-45°=15°.
∵AB=AD=AE,∠BAE=∠BAD+∠DAE=90°+60°=150°,
∴∠ABE=∠AEB=
| 180°-150° |
| 2 |
∴∠ABF=∠GDE.
又∵∠DEG=∠DEA-∠AEB=60°-15°=45°=∠BAC,DE=AD=AB,

∴△ABF≌△EDG
∴EG=AF,
∴AF+BF=EG+FG=EF.
AF+BF=EF的证明方法二(简略):
在FE上截取FG=AF,连接AG.证得△AFG为等边三角形.
证得△ABF≌△AEG.
证得AF+BF=EF.
AF2+EF2=2BF2的证明方法(简略):

作BG⊥BF,且使BG=BF,连接CG、FG,证得△BGC≌△BFA.
证得FC=FE,FG=
| 2 |
利用Rt△FCG中,得出AF2+EF2=2BF2.
点评:本题是一道考查正方形性质的几何题,考查了正方形的性质,三角形中位线的运用,全等三角形的运用,第二问的辅助线在第一问的基础上进行.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
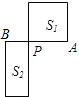 如图,已知点P是线段AB的黄金分割点,且PA>PB,若S1表示以PA为边的正方形的面积,S2表示长为AB、宽为PB的矩形的面积,那么S1( )S2.
如图,已知点P是线段AB的黄金分割点,且PA>PB,若S1表示以PA为边的正方形的面积,S2表示长为AB、宽为PB的矩形的面积,那么S1( )S2.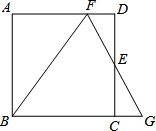 (2013•海陵区模拟)已知点E是正方形ABCD中的CD的中点,F是边AD上一点,连接FE并延长交BC延长线于点G,AB=6.
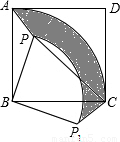
(2013•海陵区模拟)已知点E是正方形ABCD中的CD的中点,F是边AD上一点,连接FE并延长交BC延长线于点G,AB=6.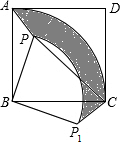 如图,已知点P是正方形ABCD内一点,连接PA、PB.将△PAB绕点B沿顺时针方向旋转90°到△P1CB的位置.设AB的长为3,PB的长为2,则△PAB旋转到△P1CB的位置的过程中,边PA所扫过的区域(图中阴影部分)的面积为
如图,已知点P是正方形ABCD内一点,连接PA、PB.将△PAB绕点B沿顺时针方向旋转90°到△P1CB的位置.设AB的长为3,PB的长为2,则△PAB旋转到△P1CB的位置的过程中,边PA所扫过的区域(图中阴影部分)的面积为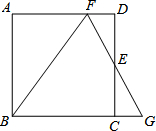 已知点E是正方形ABCD中的CD的中点,F是边AD上一点,连接FE并延长交BC延长线于点G,AB=6.
已知点E是正方形ABCD中的CD的中点,F是边AD上一点,连接FE并延长交BC延长线于点G,AB=6.