题目内容
【题目】如图1，在菱形ABCD中，E是CD上的一点，连接BE交AC于O，连接DO并延长交BC于E．
（1）求证：△FOC≌△EOC;
（2）将此图中的AD、BE分别延长交于点N，作EM∥BC交CN于M，再连接FM即得到图2．
求证：①
；②FD=FM．
【答案】
（1）
证明：∵四边形ABCD是菱形，
∴BC=CD，∠BCA=∠DCA，BC∥AD，
在△BCO和△DCO中，
，
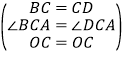∴△BCO≌△DCO（SAS），
∴∠CBO=∠CDO，
在△BEC和△DFC中，
，
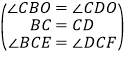∴△BEC≌△DFC（ASA），
∴EC=FC，
在△FOC和△EOC中，
，
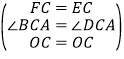∴△FOC≌△EOC（SAS）
（2）
如图2所示，
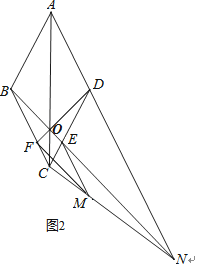
∵EM∥BC，BC∥AD，
∴EM∥BC∥AD
∴
，
，
∴
，
∵CE=CF，CD=CB
∴
，
∴
；
∵
∴FM∥BN
∵EM∥BC
∴四边形FMEB为平行四边形
∴FM=BE
∵BE=DF
∴FD=FM．
【解析】（1）可以通过多组三角形全等证得，先根据SAS证明△BCO≌△DCO，得到∠CBO=∠CDO，然后根据ASA证明△BEC≌△DFC，进而可得CF=CE，然后根据SAS即可证明△FOC≌△EOC；
（2）利用EM∥BC来转化比：，由BC∥AD，可得EM∥AD，可得，进而可得：，再利用CE=CF，CD=CB，即可得证；
由，得到FM∥BN，再利用EM∥BC，得到四边形FMEB为平行四边形，从而FM=BE=FD．
【考点精析】利用相似三角形的判定与性质和相似三角形的应用对题目进行判断即可得到答案，需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方；测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解．
