ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§Ε‘”ΎΡ≥Βψ
÷–Θ§Ε‘”ΎΡ≥Βψ![]() Θ®
Θ®![]() ≤Μ «‘≠ΒψΘ©Θ§≥Τ“‘Βψ
≤Μ «‘≠ΒψΘ©Θ§≥Τ“‘Βψ![]() ΈΣ‘≤–ΡΘ§
ΈΣ‘≤–ΡΘ§![]() ≥ΛΈΣΑκΨΕΒΡ‘≤ΈΣΒψ
≥ΛΈΣΑκΨΕΒΡ‘≤ΈΣΒψ![]() ΒΡΑκ≥Λ‘≤ΘΜΕ‘”ΎΒψ
ΒΡΑκ≥Λ‘≤ΘΜΕ‘”ΎΒψ![]() Θ§»τΫΪΒψ
Θ§»τΫΪΒψ![]() ΒΡΑκ≥Λ‘≤
ΒΡΑκ≥Λ‘≤![]() »Τ‘≠Βψ–ΐΉΣΘ§ΡήΙΜ ΙΒΟΒψ
»Τ‘≠Βψ–ΐΉΣΘ§ΡήΙΜ ΙΒΟΒψ![]() ΈΜ”ΎΒψ
ΈΜ”ΎΒψ![]() ΒΡΑκ≥Λ‘≤ΡΎ≤ΩΜρ‘≤…œΘ§‘ρ≥ΤΒψ
ΒΡΑκ≥Λ‘≤ΡΎ≤ΩΜρ‘≤…œΘ§‘ρ≥ΤΒψ![]() Ρή±ΜΒψ
Ρή±ΜΒψ![]() Ακ≥Λ≤ΕΜώΘ®ΜρΒψ
Ακ≥Λ≤ΕΜώΘ®ΜρΒψ![]() ΡήΑκ≥Λ≤ΕΜώΒψ
ΡήΑκ≥Λ≤ΕΜώΒψ![]() Θ©Θ°
Θ©Θ°
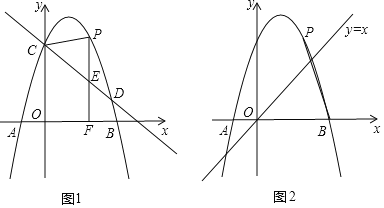
Θ®1Θ©»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§Βψ
÷–Θ§Βψ![]() Θ§‘ρΒψ
Θ§‘ρΒψ![]() ΒΡΑκ≥Λ‘≤ΒΡΟφΜΐΈΣ__________ΘΜœ¬Ν–ΗςΒψ
ΒΡΑκ≥Λ‘≤ΒΡΟφΜΐΈΣ__________ΘΜœ¬Ν–ΗςΒψ![]() ΓΔ
ΓΔ ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Θ§Ρή±ΜΒψ
Θ§Ρή±ΜΒψ![]() Ακ≥Λ≤ΕΜώΒΡΒψ”–__________ΘΜ
Ακ≥Λ≤ΕΜώΒΡΒψ”–__________ΘΜ
Θ®2Θ©“―÷ΣΒψ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§ΔΌ»γΆΦΘ§Βψ
Θ§ΔΌ»γΆΦΘ§Βψ![]() Θ§Β±
Θ§Β±![]() ±Θ§œΏΕΈ
±Θ§œΏΕΈ![]() …œΒΡΥυ”–ΒψΨυΩ…“‘±ΜΒψ
…œΒΡΥυ”–ΒψΨυΩ…“‘±ΜΒψ![]() Ακ≥Λ≤ΕΜώΘ§«σ
Ακ≥Λ≤ΕΜώΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜΔΎ»τΕ‘”ΎΤΫΟφ…œΒΡ»Έ“βΒψΘ®‘≠Βψ≥ΐΆβΘ©ΕΦ≤ΜΡήΑκ≥Λ≤ΕΜώœΏΕΈ
ΒΡ»Γ÷ΒΖΕΈßΘΜΔΎ»τΕ‘”ΎΤΫΟφ…œΒΡ»Έ“βΒψΘ®‘≠Βψ≥ΐΆβΘ©ΕΦ≤ΜΡήΑκ≥Λ≤ΕΜώœΏΕΈ![]() …œΒΡΥυ”–ΒψΘ§÷±Ϋ”–¥≥ω
…œΒΡΥυ”–ΒψΘ§÷±Ϋ”–¥≥ω![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©S=Π–Θ§BΓΔCΝΫΒψΘΜΘ®2Θ©ΔΌΘ≠2ΓήnΓή![]() Μρ
Μρ![]() Γή6nΓή2ΘΜΘ®2Θ©ΔΎ
Γή6nΓή2ΘΜΘ®2Θ©ΔΎ![]() ΘΦtΘΦ
ΘΦtΘΦ![]()
ΓΨΫβΈωΓΩ
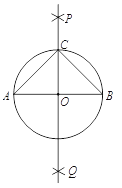
Θ®1Θ©ΗυΨίΕ®“εΘ§ΑκΨΕΈΣ1Θ§÷±Ϋ”«σΟφΜΐΘΜΗυΨί±Μ≤ΕΜώΒΡΕ®“εΘ§…ηΒψΒΫ‘≤–ΡΒΡΨύάκΈΣdΘ§÷Μ–ηrΓήdΓή3rΘ§Φ¥Ω…“‘≤ΕΜώΘΜ
Θ®2Θ©ΔΌάϊ”ΟrΓήdΓή3r’βΗω–‘÷ Θ§Ζ÷±πΦΤΥψΝΌΫγΒψΘΚΒψEΚΆΒψFΡήΙΜ±Μ≤ΕΜώΒΡΖΕΈßΘ§»ΜΚσ»ΞΙΪΙ≤≤ΩΖ÷Φ¥Ω…ΘΜ
Θ®2Θ©ΔΎ‘Ύ…œ“ΜΈ ΒΡΜυ¥Γ…œΘ§÷Μ–ηΫβΒΟΒΡ≤ΜΒ» ΫΈόΙΪΙ≤≤ΩΖ÷Θ§‘ρ≤ΜΡή≤ΕΜώ
Θ®1Θ©ΓΏΒψ![]()
Γύ‘≤ΒΡΑκΨΕΈΣ1Θ§ΟφΜΐΈΣΠ–
ΗυΨί±Μ≤ΕΜώΒΡΕ®“εΘ§…ηΒψΒΫ‘≤–ΡΒΡΨύάκΈΣdΘ§÷Μ–ηrΓήdΓή3rΘ§Φ¥Ω…“‘≤ΕΜώ
Φ¥Β±1ΓήdΓή3 ±Θ§ΒψΩ…±Μ≤ΕΜώ
![]() Θ§‘ρd=
Θ§‘ρd=![]() Θ§≤ΜΖϊΚœΘΜ
Θ§≤ΜΖϊΚœΘΜ
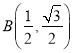 Θ§d=2Θ§ΖϊΚœΘΜ
Θ§d=2Θ§ΖϊΚœΘΜ
![]() Θ§d=2
Θ§d=2![]() Θ§ΖϊΚœΘΜ
Θ§ΖϊΚœΘΜ
![]() Θ§d=
Θ§d=![]() Θ§≤ΜΖϊΚœ
Θ§≤ΜΖϊΚœ
Θ®2Θ©ΔΌΓΏΒψN(0Θ§n)
Γύ‘≤ΒΡΑκΨΕΈΣ![]() Θ§Υυ“‘÷Μ–η¬ζΉψ
Θ§Υυ“‘÷Μ–η¬ζΉψ![]() ΓήdΓή
ΓήdΓή![]() ±Θ§‘ρΩ…±Μ≤ΕΜώ
±Θ§‘ρΩ…±Μ≤ΕΜώ
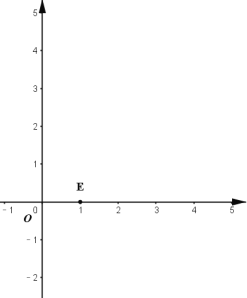
ΒψE(1Θ§0)Θ§‘ρd=1Θ§“ΣœκΡήΙΜ±Μ≤ΕΜώΘ§‘ρΘΚ
![]() Γή1Γή
Γή1Γή![]()
ΫβΒΟΘΚ![]() ΓήnΓή
ΓήnΓή![]() Μρ
Μρ![]() ΓήnΓή
ΓήnΓή![]()
ΒψF(1Θ§![]() )Θ§‘ρd=2
)Θ§‘ρd=2
Ά§άμΘ§![]() Γή2Γή
Γή2Γή![]()
ΫβΒΟΘΚ![]() ΓήnΓή
ΓήnΓή![]() Μρ
Μρ![]() ΓήnΓή
ΓήnΓή![]()
Κœ≤ΔΒΟΘΚ![]() ΓήnΓή
ΓήnΓή![]() Μρ
Μρ![]() ΓήnΓή
ΓήnΓή![]()
Θ®2Θ©ΔΎΆ§…œΘ§‘≤ΒΡΑκΨΕΈΣ![]() Θ§Υυ“‘÷Μ–η¬ζΉψ
Θ§Υυ“‘÷Μ–η¬ζΉψ![]() ΓήdΓή
ΓήdΓή![]() ±Θ§‘ρΩ…±Μ≤ΕΜώ
±Θ§‘ρΩ…±Μ≤ΕΜώ
ΒψE(tΘ§0)Θ§‘ρd=tΘ§“ΣœκΡήΙΜ±Μ≤ΕΜώΘ§‘ρΘΚ![]() ΓήnΓή
ΓήnΓή![]() Μρ
Μρ![]() ΓήnΓή
ΓήnΓή![]()
ΒψF(tΘ§![]() )Θ§‘ρd=
)Θ§‘ρd=![]() Θ§“ΣœκΡήΙΜ±Μ≤ΕΜώΘ§‘ρΘΚ
Θ§“ΣœκΡήΙΜ±Μ≤ΕΜώΘ§‘ρΘΚ![]() ΓήnΓή
ΓήnΓή![]() Μρ
Μρ![]() ΓήnΓή
ΓήnΓή![]()
ΓΏ»Έ“β÷ΒΕΦ≤ΜΡή≤ΕΜώΘ§ΓύΒΟΒΫΒΡΝΫΗω≤ΜΒ» ΫΈόΙΪΙ≤≤ΩΖ÷Θ§Φ¥ΘΚ
![]() ΚΆ
ΚΆ![]() ΘΨ
ΘΨ![]()
‘ΎΫαΚœtΘΨ0Θ§ΫβΒΟΘΚ0ΘΦtΘΦ![]()

 »ΪΡή≤βΩΊ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
»ΪΡή≤βΩΊ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΈΣΝΥΒς≤ι―ß…ζΕ‘ά§ΜχΖ÷άύΦΑΆΕΖ≈÷Σ ΕΒΡΝΥΫβ«ιΩωΘ§¥”ΦΉΓΔ““ΝΫ–ΘΗςΥφΜζ≥ι»Γ40Οϊ―ß…ζΫχ––ΝΥœύΙΊ÷Σ Ε≤β ‘Θ§ΜώΒΟΝΥΥϊΟ«ΒΡ≥…Φ®Θ®ΑΌΖ÷÷ΤΘ©Θ§≤ΔΕ‘ ΐΨίΘ®≥…Φ®Θ©Ϋχ––ΝΥ’ϊάμΓΔΟη ωΚΆΖ÷ΈωΘ°œ¬ΟφΗχ≥ωΝΥ≤ΩΖ÷–≈œΔΘ°
aΘ°ΦΉΓΔ““ΝΫ–Θ40Οϊ―ß…ζ≥…Φ®ΒΡΤΒ ΐΖ÷≤ΦΆ≥ΦΤ±μ»γœ¬ΘΚ
≥…Φ®x ―ß–Θ |
|
|
|
|
|
ΦΉ | 4 | 11 | 13 | 10 | 2 |
““ | 6 | 3 | 15 | 14 | 2 |
Θ®ΥΒΟςΘΚ≥…Φ®80Ζ÷ΦΑ“‘…œΈΣ”≈–ψΘ§70~79Ζ÷ΈΣΝΦΚΟΘ§60~69Ζ÷ΈΣΚœΗώΘ§60Ζ÷“‘œ¬ΈΣ≤ΜΚœΗώΘ©
bΘ°ΦΉ–Θ≥…Φ®‘Ύ![]() ’β“ΜΉιΒΡ «ΘΚ
’β“ΜΉιΒΡ «ΘΚ
70 70 70 71 72 73 73 73 74 75 76 77 78
cΘ°ΦΉΓΔ““ΝΫ–Θ≥…Φ®ΒΡΤΫΨυΖ÷ΓΔ÷–ΈΜ ΐΓΔ÷Ύ ΐ»γœ¬ΘΚ
―ß–Θ | ΤΫΨυΖ÷ | ÷–ΈΜ ΐ | ÷Ύ ΐ |
ΦΉ | 74.2 | n | 5 |
““ | 73.5 | 76 | 84 |
ΗυΨί“‘…œ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©–¥≥ω±μ÷–nΒΡ÷ΒΘΜ
Θ®2Θ©‘Ύ¥Υ¥Έ≤β ‘÷–Θ§Ρ≥―ß…ζΒΡ≥…Φ® «74Ζ÷Θ§‘ΎΥϊΥυ τ―ß–Θ≈≈‘Ύ«Α20ΟϊΘ§”…±μ÷– ΐΨίΩ…÷ΣΗΟ―ß…ζ «_____________–ΘΒΡ―ß…ζΘ®ΧνΓΑΦΉΓ±ΜρΓΑ““Γ±Θ©Θ§άμ”… «__________ΘΜ
Θ®3Θ©ΦΌ…η““–Θ800Οϊ―ß…ζΕΦ≤ΈΦ”¥Υ¥Έ≤β ‘Θ§ΙάΦΤ≥…Φ®”≈–ψΒΡ―ß…ζ»Υ ΐΘ°