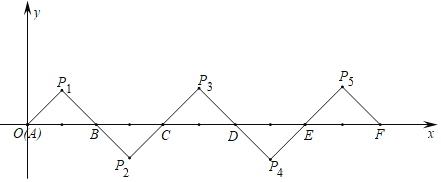
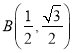ƒøƒ⁄»ð
°æƒø°ø»ÁÕº1À˘ 棨≈◊ŒÔœþ![]() ”Î
”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() ¡Ωµ„£¨”Î
¡Ωµ„£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨÷±œþ
£¨÷±œþ![]() æ≠π˝µ„
æ≠π˝µ„![]() £¨”Î≈◊ŒÔœþ¡Ì“ª∏ˆΩªµ„Œ™
£¨”Î≈◊ŒÔœþ¡Ì“ª∏ˆΩªµ„Œ™![]() £¨µ„
£¨µ„![]() «≈◊ŒÔœþ…œµƒ“ª∏ˆ∂ص„£¨π˝
«≈◊ŒÔœþ…œµƒ“ª∏ˆ∂ص„£¨π˝![]() µ„◊˜
µ„◊˜![]() ÷·”⁄µ„
÷·”⁄µ„![]() £¨Ωª÷±œþ
£¨Ωª÷±œþ![]() ”⁄µ„
”⁄µ„![]()
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω
£®2£©µ±µ„![]() ‘⁄÷±œþ
‘⁄÷±œþ![]() …œ∑Ω£¨«“
…œ∑Ω£¨«“![]() «“‘
«“‘![]() Œ™—¸µƒµ»—¸»˝Ω«–Œ ±£¨«Û
Œ™—¸µƒµ»—¸»˝Ω«–Œ ±£¨«Û![]() µƒ◊¯±Í
µƒ◊¯±Í
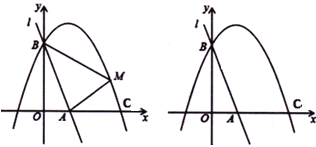
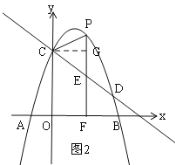
£®3£©»ÁÕº2À˘ 棨»Ùµ„![]() Œ™∂‘≥∆÷·”“≤ý≈◊ŒÔœþ…œ“ªµ„£¨¡¨Ω”
Œ™∂‘≥∆÷·”“≤ý≈◊ŒÔœþ…œ“ªµ„£¨¡¨Ω”![]() £¨“‘
£¨“‘![]() Œ™÷±Ω«∂•µ„£¨œþ∂Œ
Œ™÷±Ω«∂•µ„£¨œþ∂Œ![]() Œ™Ωœ≥§÷±Ω«±þ£¨ππ‘Ï¡Ω÷±Ω«±þ±»Œ™
Œ™Ωœ≥§÷±Ω«±þ£¨ππ‘Ï¡Ω÷±Ω«±þ±»Œ™![]() µƒ
µƒ![]() £¨ «∑ҥʑ⁄µ„
£¨ «∑ҥʑ⁄µ„![]() £¨ πµ„
£¨ πµ„![]() «°∫√¬‰‘⁄÷±œþ
«°∫√¬‰‘⁄÷±œþ![]() …œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆœý”¶µ„
…œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆœý”¶µ„![]() µƒ∫·◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ∫·◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©P
£ª£®2£©P ![]() ªÚ
ªÚ![]() £ª£®3£©¥Ê‘⁄£¨2ªÚ
£ª£®3£©¥Ê‘⁄£¨2ªÚ![]()
°æΩ‚Œˆ°ø
£®1£©¿˚”√¥˝∂®œµ ˝∑®«Û∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ Ω£ª
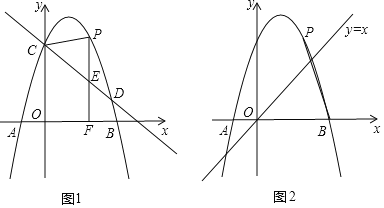
£®2£©œ»∞—Cµ„¥˙»Î÷±œþCD÷–«Û≥ˆmµƒ÷µ£¨±Ì æP(m£¨-m2+2m+3)°¢E(m£¨![]() m+3)£¨µ±°˜CPE «“‘CEŒ™—¸µƒµ»—¸»˝Ω«–Œ ±£¨»ª∫Û∑÷∑÷¡Ω÷÷«Èøˆ£∫¢Ÿµ±CE=CP ±£¨¢⁄µ±CE=PE ±£ª
m+3)£¨µ±°˜CPE «“‘CEŒ™—¸µƒµ»—¸»˝Ω«–Œ ±£¨»ª∫Û∑÷∑÷¡Ω÷÷«Èøˆ£∫¢Ÿµ±CE=CP ±£¨¢⁄µ±CE=PE ±£ª
£®3£©œ»∏˘æðµ„P‘⁄≈◊ŒÔœþ…œ£¨G‘⁄÷±œþy=x…œ…ËP(m£¨-m2+2m+3)£¨G(a£¨a)£¨
»ÁÕº3£¨◊˜∏®÷˙œþ£¨ππΩ®¡Ω∏ˆœýÀ∆»˝Ω«–Œ£¨÷§√˜°˜PHG°◊°˜BNP£¨‘Ú![]() £¨”…¡Ω÷±Ω«±þ±»Œ™1£∫2¡–∑Ω≥Ã◊ÈΩ‚≥ˆ∫·◊¯±Ím£ª»ÁÕº4£¨Õ¨¿Ì¡–∑Ω≥Ã◊ÈΩ‚≥ˆmµƒ÷µ£Æ
£¨”…¡Ω÷±Ω«±þ±»Œ™1£∫2¡–∑Ω≥Ã◊ÈΩ‚≥ˆ∫·◊¯±Ím£ª»ÁÕº4£¨Õ¨¿Ì¡–∑Ω≥Ã◊ÈΩ‚≥ˆmµƒ÷µ£Æ
Ω‚£∫£®1£©∞—µ„![]() µƒ◊¯±Í¥˙»Î≈◊ŒÔœþ
µƒ◊¯±Í¥˙»Î≈◊ŒÔœþ![]() ÷–£¨
÷–£¨
µ√£∫![]() £¨
£¨
Ω‚µ√![]() £¨
£¨
À˘“‘≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™![]() £ª
£ª
£®2£©∞—![]() ¥˙»Î
¥˙»Î![]() £¨µ√
£¨µ√![]() £¨
£¨
À˘“‘÷±œþµƒΩ‚Œˆ ΩŒ™£∫![]() £¨
£¨
…Ë![]() £¨
£¨
¢Ÿµ±![]() ±£¨◊˜
±£¨◊˜![]() £¨»ÁÕº2£¨
£¨»ÁÕº2£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £Æ
£Æ
![]() £¨
£¨
![]() £¨
£¨
µ±![]() ±£¨
±£¨![]() £ª
£ª
¢⁄µ±![]() ±£¨
±£¨ ![]() £¨
£¨![]() £¨
£¨
π¥π…∂®¿Ìµ√![]() £¨
£¨
![]() £¨
£¨
Ω‚µ√![]() (…·»•)£¨
(…·»•)£¨![]() £¨
£¨
µ±![]() ±
±![]() £¨
£¨
◊€…œÀ˘ ˆµ±»˝Ω«–Œ![]() «“‘
«“‘![]() Œ™—¸µƒµ»—¸»˝Ω«–Œ ±£¨µ„Pµƒ◊¯±ÍŒ™
Œ™—¸µƒµ»—¸»˝Ω«–Œ ±£¨µ„Pµƒ◊¯±ÍŒ™![]() ªÚ
ªÚ![]() £ª
£ª
£®3£©µ„Pµƒ∫·◊¯±ÍŒ™2ªÚ![]() £Æ
£Æ
…ËP(m£¨-m2+2m+3)£¨G(a£¨a)£¨
»ÁÕº3£¨
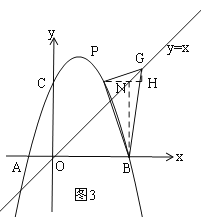
π˝B◊˜BN°Œy÷·£¨π˝P◊˜PH°Œx÷·£¨Ωª”⁄N£¨π˝G◊˜GH°ÕPN£¨¥π◊„Œ™H£¨‘Ú°œPHG=°œBNP=90°„£¨
°ý°œNBP+°œBPN=90°„£¨
°þ°œBPG=90°„£¨
°ý°œBPN+°œNPG=90°„£¨
°ý°œNBP=°œNPG£¨
°ý°˜PHG°◊°˜BNP£¨
°ý![]() £¨
£¨
°þ![]() =2£¨
=2£¨
°ý![]() =2£¨
=2£¨
°ý![]() =2£¨
=2£¨
‘Ú £¨
£¨
Ω‚µ√£∫m1=-3£®…·»•£©£¨m2=2£ª
»ÁÕº4£¨
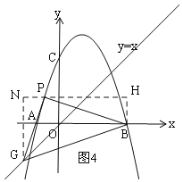
π˝P◊˜NH°Œx÷·£¨π˝G◊˜GN°ÕNH£¨π˝B◊˜BH°ÕNH£¨¥π◊„∑÷±Œ™N°¢H£¨
Õ¨¿Ìµ√£∫°˜PNG°◊°˜BHP£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
°ý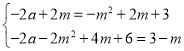 £¨
£¨
Ω‚µ√£∫m1=![]() £®…·»•£©£¨m2=
£®…·»•£©£¨m2=![]() £¨
£¨
◊€…œÀ˘ ˆ£¨œý”¶µ„Pµƒ∫·◊¯±ÍŒ™2ªÚ![]() £Æ
£Æ

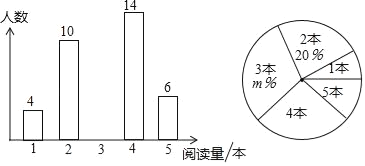
°æƒø°ø—ß–£ø™’π°∞ Èœ„–£‘∞°±ªÓ∂Ø“‘¿¥£¨ еΩÕ¨—ß√«µƒπ„∑∫πÿ◊¢£¨—ß–£Œ™¡ÀΩ‚»´–£—ß…˙øŒÕ‚‘ƒ∂¡µƒ«Èøˆ£¨Àʪ˙µ˜≤È¡À≤ø∑÷—ß…˙‘⁄“ª÷Ѓ⁄ΩË‘ƒÕº ȵƒ¥Œ ˝£¨≤¢÷∆≥…»ÁÕº≤ªÕÍ’˚µƒÕ≥º∆±Ì
—ß…˙ΩË‘ƒÕº ȵƒ¥Œ ˝
ΩË‘ƒÕº ȵƒ¥Œ ˝ | 0¥Œ | 1¥Œ | 2¥Œ | 3¥Œ | 4¥Œº∞“‘…œ |
»À ˝ | 7 | 13 | a | 10 | 3 |
—ß…˙ΩË‘ƒÕº ȵƒ¥Œ ˝Õ≥º∆±Ì

«Îƒ„∏˘æðÕ≥º∆Õº±Ìµƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©a= £ªb=
£®2£©∏√µ˜≤ÈÕ≥º∆ ˝æðµƒ÷–Œª ˝ «__________¥Œ
£®3£©…»–ŒÕ≥º∆Õº÷–£¨°∞3¥Œ°±À˘∂‘”¶µƒ…»–Œ‘≤–ƒΩ«∂» ˝ «______________£ª
£®4£©»Ù∏√–£π≤”–2000√˚—ß…˙£¨∏˘æðµ˜≤ÈΩ·π˚£¨π¿º∆∏√–£—ß…˙‘⁄“ª÷Ѓ⁄ΩË‘ƒÕº È°∞4¥Œ“‘…œ°±µƒ»À ˝