题目内容
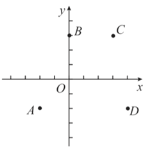
【题目】在平面直角坐标系![]() 中,存在抛物线
中,存在抛物线![]() 以及两点
以及两点![]() 和
和![]() .
.
(1)求该抛物线的顶点坐标;
(2)若该抛物线经过点![]() ,求此抛物线的表达式;
,求此抛物线的表达式;
(3)若该抛物线与线段![]() 只有一个公共点,结合图象,求
只有一个公共点,结合图象,求![]() 的取值范围.
的取值范围.
【答案】(1)(0,2);(2)![]() ;(3)m=2或
;(3)m=2或![]() .
.
【解析】
(1)![]() 是顶点式,可得到结论;
是顶点式,可得到结论;
(2)把A点坐标代入![]() 得方程,于是得到结论;
得方程,于是得到结论;
(3)分两种情况:当抛物线开口向上或向下时,分别画出图形,找到临界位置关系,求出m的值,再进行分析变化趋势可得到结论.
(1)![]() 是顶点式,顶点坐标为
是顶点式,顶点坐标为![]() ;
;
(2)∵抛物线经过点![]() ,
,
∴m=9m +2,
解得: ![]() ,
,
∴![]()
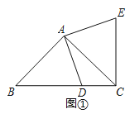
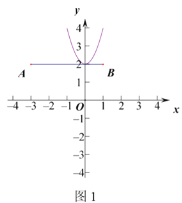
(3)如图1,当抛物线开口向上时,抛物线顶点在线段![]() 上时,
上时,![]() ;
;
当m>2时,直线x=1交抛物线于点(1,m+2),交点位于点B上方,所以此时线段![]() 与抛物线一定有两个交点,不符合题意;
与抛物线一定有两个交点,不符合题意;
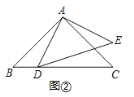
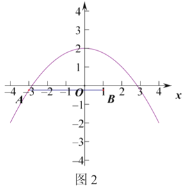
如图2,当抛物线开口向下时,抛物线顶过点![]() 时,
时,![]() ;
;
直线x=-3交抛物线于点(-3,9m+2),当![]() 时,9m+2<m,交点位于点A下方,直线x=1交抛物线于点(1,m+2),交点位于点B上方,所以此时线段
时,9m+2<m,交点位于点A下方,直线x=1交抛物线于点(1,m+2),交点位于点B上方,所以此时线段![]() 与抛物线一定有且只有一个交点,符合题意;
与抛物线一定有且只有一个交点,符合题意;
综上所述,当![]() 或
或![]() 时,抛物线与线段
时,抛物线与线段![]() 只有一个公共点.
只有一个公共点.

练习册系列答案
相关题目