题目内容
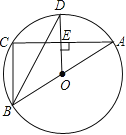
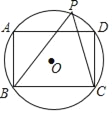
【题目】如图，矩形ABCD内接于⊙O，点P是
上一点，连接PB、PC，若AD=2AB，则cos∠BPC的值为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
连接BD，根据圆周角定理可得cos∠BDC=cos∠BPC，又BD为直径，则∠BCD=90°，设DC为x，则BC为2x，根据勾股定理可得BD=
x，再根据cos∠BDC=
=
=
，即可得出结论.
连接BD，
∵四边形ABCD为矩形，
∴BD过圆心O，
∵∠BDC=∠BPC（圆周角定理）
∴cos∠BDC=cos∠BPC
∵BD为直径，
∴∠BCD=90°，
∵
=
,
∴设DC为x，
则BC为2x，
∴BD=
=
=x，
∴cos∠BDC===，
∵cos∠BDC=cos∠BPC，
∴cos∠BPC=.
故答案选A.
练习册系列答案
相关题目
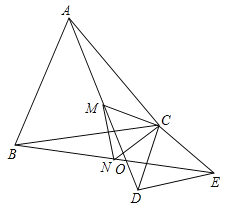
【题目】已知：如图，
、
都是等腰三角形，且
，
，
，
、
相交于点
，点
、
分别是线段、的中点．以下4个结论：①
；②
；③
是等边三角形；④连
，则平分
以上四个结论中正确的是：______．（把所有正确结论的序号都填上）
【题目】某市扶贫办在精准扶贫工作中，组织30辆汽车装运花椒、核桃、甘蓝向外地销售．按计划30辆车都要装运，每辆汽车只能装运同一种产品，且必须装满，根据下表提供的信息，解答以下问题：
产品名称 | 核桃 | 花椒 | 甘蓝 |
每辆汽车运载量（吨） | 10 | 6 | 4 |
每吨土特产利润（万元） | 0.7 | 0.8 | 0.5 |
若装运核桃的汽车为x辆，装运甘蓝的车辆数是装运核桃车辆数的2倍多1，假设30辆车装运的三种产品的总利润为y万元．
(1)求y与x之间的函数关系式；
(2)若装花椒的汽车不超过8辆，求总利润最大时，装运各种产品的车辆数及总利润最大值．
