题目内容
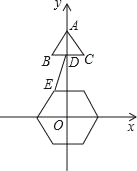
【题目】如图，已知边长为2的正三角形ABC顶点A的坐标为（0，6），BC的中点D在y轴上，且在点A下方，点E是边长为2、中心在原点的正六边形的一个顶点，把这个正六边形绕中心旋转一周，在此过程中DE的最小值为（ ）
A. 3 B. 4﹣
C. 4 D. 6﹣2
【答案】B
【解析】
首先得到当点E旋转至y轴上时DE最小，然后分别求得AD、OE′的长，最后求得DE′的长即可．
如图，当点E旋转至y轴上时DE最小；
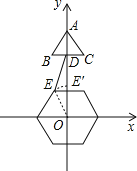
∵△ABC是等边三角形，D为BC的中点，
∴AD⊥BC
∵AB=BC=2
∴AD=ABsin∠B=
，
∵正六边形的边长等于其半径，正六边形的边长为2，
∴OE=OE′=2
∵点A的坐标为（0，6）
∴OA=6
∴DE′=OA-AD-OE′=4-
故选B．
练习册系列答案
名校课堂系列答案
相关题目
