题目内容
【题目】平面直角坐标系xOy中,点A、B分别在函数y1= ![]() (x>0)与y2=﹣
(x>0)与y2=﹣ ![]() (x<0)的图象上,A、B的横坐标分别为
(x<0)的图象上,A、B的横坐标分别为
a、b.
(1)若AB∥x轴,求△OAB的面积;
(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值;
(3)作边长为3的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于4的任意实数a,CD边与函数y1= ![]() (x>0)的图象都有交点,请说明理由.
(x>0)的图象都有交点,请说明理由.
【答案】
(1)
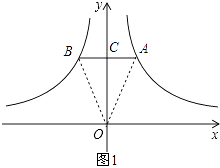
解:如图1,AB交y轴于C,
∵AB∥x轴,
∴S△OAC= ![]() ×|4|=2,S△OBC=
×|4|=2,S△OBC= ![]() ×|﹣4|=2,
×|﹣4|=2,
∴S△OAB=S△OAC+S△OBC=4;
(2)
解:∵A、B的横坐标分别为a、b,
∴A、B的纵坐标分别为 ![]() 、﹣
、﹣ ![]() ,
,
∴OA2=a2+( ![]() )2,OB2=b2+(﹣
)2,OB2=b2+(﹣ ![]() )2,
)2,
∵△OAB是以AB为底边的等腰三角形,
∴OA=OB,
∴a2+( ![]() )2=b2+(﹣
)2=b2+(﹣ ![]() )2,
)2,
∴a2﹣b2+( ![]() )2﹣(
)2﹣( ![]() )2=0,
)2=0,
∴a2﹣b2+ ![]() =0,
=0,
∴(a+b)(a﹣b)(1﹣ ![]() )=0,
)=0,
∵a+b≠0,a>0,b<0,
∴1﹣ ![]() =0,
=0,
∴ab=﹣4;
(3)
解:∵a≥4,
而AC=3,
∴直线CD在y轴的右侧,直线CD与函数y1= ![]() (x>0)的图象一定有交点,
(x>0)的图象一定有交点,
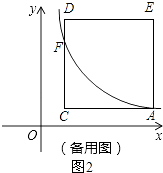
设直线CD与函数y1= ![]() (x>0)的图象交点为F,如图2,
(x>0)的图象交点为F,如图2,
∵A点坐标为(a, ![]() ),正方形ACDE的边长为3,
),正方形ACDE的边长为3,
∴C点坐标为(a﹣3, ![]() ),
),
∴F点的坐标为(a﹣3, ![]() ),
),
∴FC= ![]() ﹣
﹣ ![]() ,
,
∵3﹣FC=3﹣( ![]() ﹣
﹣ ![]() )=
)= ![]() ,
,
而a≥4,
∴3﹣FC≥0,即FC≤3,
∵CD=3,
∴点F在线段DC上,
即对大于或等于4的任意实数a,CD边与函数y1= ![]() (x>0)的图象都有交点.
(x>0)的图象都有交点.
【解析】(1)如图1,AB交y轴于C,由于AB∥x轴,根据k的几何意义得到S△OAC=2,S△OBC=2,所以S△OAB=S△OAC+S△OBC=4;(2)根据函数图象上点的坐标特征得A、B的纵坐标分别为 ![]() 、﹣
、﹣ ![]() ,根据两点间的距离公式得到OA2=a2+(
,根据两点间的距离公式得到OA2=a2+( ![]() )2 , OB2=b2+(﹣
)2 , OB2=b2+(﹣ ![]() )2 , 则利用等腰三角形的性质得到a2+(
)2 , 则利用等腰三角形的性质得到a2+( ![]() )2=b2+(﹣
)2=b2+(﹣ ![]() )2 , 变形得到(a+b)(a﹣b)(1﹣
)2 , 变形得到(a+b)(a﹣b)(1﹣ ![]() )=0,由于a+b≠0,a>0,b<0,所以1﹣
)=0,由于a+b≠0,a>0,b<0,所以1﹣ ![]() =0,易得ab=﹣4;(3)由于a≥4,AC=3,则可判断直线CD在y轴的右侧,直线CD与函数y1=
=0,易得ab=﹣4;(3)由于a≥4,AC=3,则可判断直线CD在y轴的右侧,直线CD与函数y1= ![]() (x>0)的图象一定有交点,设直线CD与函数y1=
(x>0)的图象一定有交点,设直线CD与函数y1= ![]() (x>0)的图象交点为F,由于A点坐标为(a,
(x>0)的图象交点为F,由于A点坐标为(a, ![]() ),正方形ACDE的边长为3,则得到C点坐标为(a﹣3,
),正方形ACDE的边长为3,则得到C点坐标为(a﹣3, ![]() ),F点的坐标为(a﹣3,
),F点的坐标为(a﹣3, ![]() ),所以FC=
),所以FC= ![]() ﹣
﹣ ![]() ,然后比较FC与3的大小,由于3﹣FC=3﹣(
,然后比较FC与3的大小,由于3﹣FC=3﹣( ![]() ﹣
﹣ ![]() )=
)= ![]() ,而a≥4,所以3﹣FC≥0,于是可判断点F在线段DC上.
,而a≥4,所以3﹣FC≥0,于是可判断点F在线段DC上.
【考点精析】认真审题,首先需要了解反比例函数的图象(反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点),还要掌握反比例函数的性质(性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大)的相关知识才是答题的关键.




