题目内容
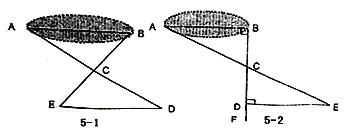
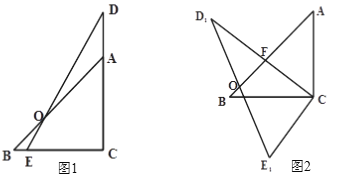
【题目】把两个直角三角形如图(1)放置,使∠ACB与∠DCE重合,AB与DE相交于点O,其中∠DCE=90°,∠BAC=45°,AB=6![]() cm,CE=5cm, CD=10cm.
cm,CE=5cm, CD=10cm.
(1)图1中线段AO的长= cm;DO=cm
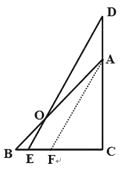
(2)如图2,把△DCE绕着点C逆时针旋转α度(0°<α<90°)得△D1CE1,D1C与AB相交于点F,若△BCE1恰好是以BC为底边的等腰三角形,求线段AF的长.
【答案】(1)AO=![]() cm;DO=
cm;DO=![]() cm; (2)
cm; (2)![]() .
.
【解析】
试题(1)作![]() ,利用三角形相似来求出线段AO ,DO的长;
,利用三角形相似来求出线段AO ,DO的长;
(2)连接BE1,过点E1作E1G⊥BC于G, 过点F作FH⊥BC于H,根据三角形相似求出BF,即可得到答案.
试题解析:(1)如图,过点A作![]() ,
,
∵∠ACB与∠DCE重合,∠DCE=90°,∠BAC=45°,AB=![]() ,
,
∴AC=BC=6,
∵∠DCE="90°,CE=5," CD=10.
∴ED=![]() , BE=BC-CE=6-5=1,AD=CD-AC=10-6=4,
, BE=BC-CE=6-5=1,AD=CD-AC=10-6=4,
∵![]()
∴△AFC∽△DEC
∴![]() ,即AF=
,即AF=![]() ,
,
∴![]() ,即EF=2,
,即EF=2,
∴BF=EF+BE=2+1=3,
∵![]()
∴△BOE∽△BAF
∴![]() ,即AO=
,即AO=![]()
![]() ,即OE=
,即OE=![]()
∴DO=DE-OE=![]()
(2) 连接BE1,过点E1作E1G⊥BC于G, 过点F作FH⊥BC于H,
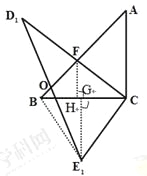
∵△DCE绕着点C 逆时针旋转α度
∴∠E1CG=α,
∵△BCE1恰好是以BC为底边的等腰三角形,
∴E1G是线段BC的中垂线
∵E1C=5,BC=6
∴CG=BH=3,![]() ,
,
∵FH⊥BC,∠DCE=90°,∠BAC=45°,
∴BH=FH,令BH=FH=x,
则:CH=6-x
在△FHC与△CG E1中
∵∠E1CG +∠FCH=∠FCH +∠CFH=90°,
∴∠E1CG =∠CFH,
∵∠FHC=∠CG E1=90°,
∴△FHC∽△CG E1,
∴![]() ,即:
,即:![]() ,解得
,解得![]() ,
,
∴FH=![]() ,
,
∵∠FHB=90°,∠BAC=45°,
∴![]()
∴![]() .
.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案