题目内容
【题目】小慧根据学习函数的经验,对函数![]() 的图像与性质进行了探究.下面是小慧的探究过程,请补充完整.
的图像与性质进行了探究.下面是小慧的探究过程,请补充完整.
(l)函数![]() 的自变量
的自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)列表,找出![]() 与
与![]() 的几组对应值.
的几组对应值.

其中,![]() ;
;
(3)在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点,并画出该函数的图像;
中,描出以上表中各对对应值为坐标的点,并画出该函数的图像;
(4)写出该函数的一条性质: .
【答案】(1)![]() 为任意数;(2)
为任意数;(2)![]() ;(3)详见解析;(4)①函数的最小值为0或
;(3)详见解析;(4)①函数的最小值为0或![]() ;②对称轴为直线
;②对称轴为直线![]() ;③
;③![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
【解析】
(1)根据一次函数的性质即可得出结论;
(2)把x=-1代入函数解析式,求出y的值即可;
(3)在坐标系内描出各点,再顺次连接即可;
(4)根据函数图象即可得出结论.
(1)∵x无论为何值,函数均有意义,
∴x为任意实数.
故答案为:任意实数;
(2)∵当x=-1时,y=|-1-1|=2,
∴b=2.
故答案为:2;
(3)如图所示;
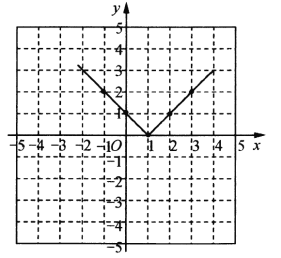
(4)①函数的最小值为0或![]()
②对称轴为直线![]()
③![]() 时,
时,![]() 随
随![]() 的增大而增大,
的增大而增大,![]() 时,
时,![]() 随
随![]() 的增大而减小. (答案不唯一,写出一条即可)
的增大而减小. (答案不唯一,写出一条即可)

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
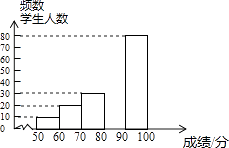
浙江新课程三维目标测评课时特训系列答案【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b=;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?