题目内容
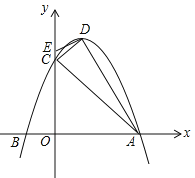
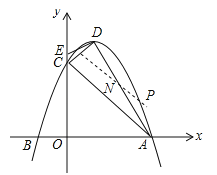
【题目】已知,抛物线![]() (a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=
(a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=![]() .
.
(1)求抛物线的解析式及顶点D的坐标;
(2)求证:直线DE是△ACD外接圆的切线;
(3)在直线AC上方的抛物线上找一点P,使![]() ,求点P的坐标;
,求点P的坐标;
(4)在坐标轴上找一点M,使以点B、C、M为顶点的三角形与△ACD相似,直接写出点M的坐标.
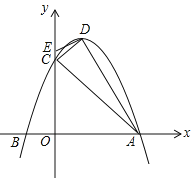
【答案】(1)![]() ,顶点D(1,4);(2)证明见解析;(3)P(
,顶点D(1,4);(2)证明见解析;(3)P(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(4)(0,0)或(9,0)或(0,﹣
);(4)(0,0)或(9,0)或(0,﹣![]() ).
).
【解析】
试题(1)由对称轴求出B的坐标,由待定系数法求出抛物线解析式,即可得出顶点D的坐标;
(2)由勾股定理和勾股定理的逆定理证出△ACD为直角三角形,∠ACD=90°.得出AD为△ACD外接圆的直径,再证明△AED为直角三角形,∠ADE=90°.得出AD⊥DE,即可得出结论;
(3)求出直线AC的解析式,再求出线段AD的中点N的坐标,过点N作NP∥AC,交抛物线于点P,求出直线NP的解析式,与抛物线联立,即可得出答案;
(4)由相似三角形的性质和直角三角形的性质即可得出答案.
试题解析:(1)∵抛物线的对称轴是直线x=1,点A(3,0),∴根据抛物线的对称性知点B的坐标为(﹣1,0),OA=3,将A(3,0),B(﹣1,0)代入抛物线解析式中得:![]() ,解得:
,解得:![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ;当x=1时,y=4,∴顶点D(1,4).
;当x=1时,y=4,∴顶点D(1,4).
(2)当=0时,∴点C的坐标为(0,3),∴AC=![]() =
=![]() ,CD=
,CD=![]() =
=![]() ,AD=
,AD=![]() =
=![]() ,∴AC2+CD2=AD2,∴△ACD为直角三角形,∠ACD=90°,∴AD为△ACD外接圆的直径,∵点E在 轴C点的上方,且CE=
,∴AC2+CD2=AD2,∴△ACD为直角三角形,∠ACD=90°,∴AD为△ACD外接圆的直径,∵点E在 轴C点的上方,且CE=![]() ,∴E(0,
,∴E(0,![]() ),∴AE=
),∴AE=![]() =
=![]() ,DE=
,DE=![]() =
=![]() ,∴DE2+AD2=AE2,∴△AED为直角三角形,∠ADE=90°,∴AD⊥DE,又∵AD为△ACD外接圆的直径,∴DE是△ACD外接圆的切线;
,∴DE2+AD2=AE2,∴△AED为直角三角形,∠ADE=90°,∴AD⊥DE,又∵AD为△ACD外接圆的直径,∴DE是△ACD外接圆的切线;
(3)设直线AC的解析式为y=kx+b,根据题意得:![]() ,解得:
,解得:![]() ,∴直线AC的解析式为y=﹣x+3,∵A(3,0),D(1,4),∴线段AD的中点N的坐标为(2,2),过点N作NP∥AC,交抛物线于点P,设直线NP的解析式为y=﹣x+c,则﹣2+c=2,解得:c=4,∴直线NP的解析式为y=﹣x+4,由y=﹣x+4,y=﹣x2+2x+3联立得:﹣x2+2x+3=﹣x+4,解得:x=
,∴直线AC的解析式为y=﹣x+3,∵A(3,0),D(1,4),∴线段AD的中点N的坐标为(2,2),过点N作NP∥AC,交抛物线于点P,设直线NP的解析式为y=﹣x+c,则﹣2+c=2,解得:c=4,∴直线NP的解析式为y=﹣x+4,由y=﹣x+4,y=﹣x2+2x+3联立得:﹣x2+2x+3=﹣x+4,解得:x=![]() 或x=
或x=![]() ,∴y=
,∴y=![]() ,或y=
,或y=![]() ,∴P(
,∴P(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(4)分三种情况:①M恰好为原点,满足△CMB∽△ACD,M(0,0);
②M在x轴正半轴上,△MCB∽△ACD,此时M(9,0);
③M在y轴负半轴上,△CBM∽△ACD,此时M(0,﹣![]() );
);
综上所述,点M的坐标为(0,0)或(9,0)或(0,﹣![]() ).
).

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案