题目内容
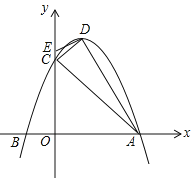
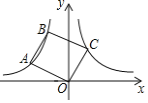
【题目】如图,点A、B在双曲线![]() (x<0)上,连接OA、AB,以OA、AB为边作OABC.若点C恰落在双曲线
(x<0)上,连接OA、AB,以OA、AB为边作OABC.若点C恰落在双曲线![]() (x>0)上,此时OABC的面积为( ).
(x>0)上,此时OABC的面积为( ).
A.![]() B.
B.![]() C.
C.![]() D.4
D.4![]()
【答案】B
【解析】
连接AC,过A作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,利用AAS证出△ABF≌△COE,设A(a,﹣![]() ),C(b,
),C(b,![]() ),则OE=BF=b,CE=AF=
),则OE=BF=b,CE=AF=![]() ,即可表示出点B的坐标,然后代入反比例函数的解析式中即可求出
,即可表示出点B的坐标,然后代入反比例函数的解析式中即可求出![]() ,然后根据平行四边形OABC的面积=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可求出结论.
,然后根据平行四边形OABC的面积=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可求出结论.
解:如图,连接AC,过A作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,

∵FD⊥x轴,CE⊥x轴
∴FD∥CE
∴∠FAC=∠ECA
∵四边形AOCB是平行四边形
∴BA∥OC,BA=OC,∠BAC=∠OCA
∴∠FAB=∠FAC-∠BAC=∠ECA-∠OCA=∠ECO
在△ABF和△COE中
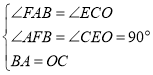
∴△ABF≌△COE,
设A(a,﹣![]() ),C(b,
),C(b,![]() ),则OE=BF=b,CE=AF=
),则OE=BF=b,CE=AF=![]() ,
,
∴B(a+b,﹣![]() ),
),
又∵点B在双曲线y=-![]() (x<0)上,
(x<0)上,
∴(a+b)(﹣![]() )=﹣3,
)=﹣3,
∴![]() ﹣
﹣![]() =2,
=2,
设![]() =x,则方程
=x,则方程![]() ﹣
﹣![]() =2可化为3x﹣
=2可化为3x﹣![]() =2,
=2,
解得x=![]() 或x=
或x=![]() (a和b异号,故舍去),
(a和b异号,故舍去),
∴![]() =
=![]() ,
,
∴![]() =﹣
=﹣![]() ,
,
∴平行四边形OABC的面积=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)
=2[![]() (﹣
(﹣![]() )(b﹣a)﹣
)(b﹣a)﹣![]() ×|﹣3|﹣
×|﹣3|﹣![]() ×|2|]
×|2|]
=﹣![]() +3+2﹣
+3+2﹣![]() ﹣5
﹣5
=﹣3×![]() ﹣2×(﹣
﹣2×(﹣![]() )
)
=2![]() .
.
故选B.

练习册系列答案
相关题目