题目内容
【题目】为落实“绿水青山就是金山银山”的发展理念,某县政府部门决定,招标一工程队负责完成一座水库的土方施工任务.该工程队有A,B两种型号的挖掘机,已知1台A型和2台B型挖掘机同时施工1小时共挖土80立方米,2台A型和3台B型挖掘机同时施工1小时共挖土140立方米.每台A型挖掘机一个小时的施工费用是350元,每台B型挖掘机一个小时的施工费用是200元.
(1)分别求每台A型,B型挖掘机一小时各挖土多少立方米?
(2)若A型和B型挖掘机共10台同时施工4小时,至少完成1360立方米的挖土量,且总费用不超过14000元.问施工时有哪几种调配方案?且指出哪种调配方案的施工费用最低,最低费用多少元?
【答案】(1) 每台A型挖掘机一小时挖土40立方米,每台B型挖掘机一小时挖土20立方米;(2) 当m=7时,即选择方案: 调配7台A型、3台B型挖掘机施工时,w取得最大值,最大值为12200元
【解析】
(1)设每台A型挖掘机一小时挖土x立方米,每台B型挖掘机一小时挖土y立方米,根据“1台A型和2台B型挖掘机同时施工1小时共挖土80立方米,2台A型和3台B型挖掘机同时施工1小时共挖土140立方米”,可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设有m台A型挖掘机参与施工,施工总费用为w元,则有(10﹣m)台B型挖掘机参与施工,由4小时至少完成1360立方米的挖土量且总费用不超过14000元,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,进而可得出各调配方案,再由施工总费用=每台挖掘机所需费用×调配台数×工作时间,即可得出w关于m的函数关系式,再利用一次函数的性质即可解决最值问题.
解:(1)设每台A型挖掘机一小时挖土x立方米,每台B型挖掘机一小时挖土y立方米,
依题意,得:![]() ,
,
解得:![]() .
.
答:每台A型挖掘机一小时挖土40立方米,每台B型挖掘机一小时挖土20立方米.
(2)设有m台A型挖掘机参与施工,施工总费用为w元,则有(10﹣m)台B型挖掘机参与施工,
∵4小时至少完成1360立方米的挖土量,且总费用不超过14000元,
∴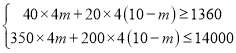 ,
,
解得:7≤m≤10.
∴共有四种调配方案,①调配7台A型、3台B型挖掘机施工;②调配8台A型、2台B型挖掘机施工;③调配9台A型、1台B型挖掘机施工;④调配10台A型挖掘机施工.
依题意,得:w=350×4m+200×4(10﹣m)=600m+8000,
∵600>0,
∴w的值随m的增大而增大,
∴当m=7时,即选择方案①时,w取得最小值,最小值为12200元.