ЬтФПФкШн
ЁОЬтФПЁПЁїABCКЭЁїEFGЪЧСНПщЭъШЋжиКЯЕФЕШБпШ§НЧаЮжНЦЌЃЌ(ШчЭМЂйЫљЪО)OЪЧAB(ЛђEF)ЕФжаЕуЃЌЁїABCВЛЖЏЃЌНЋЁїEFGШЦOЕуЫГЪБеызЊІСЉz0ЁуЃМІСЃМ120ЁуЉ{НЧЃЎ
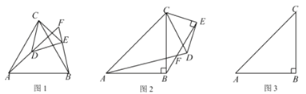
ЃЈ1ЃЉЪдЗжБ№ЫЕУїІСЮЊЖрЩйЖШЪБЃЌЕуFдкЁїABCЭтВПЁЂBCЩЯЁЂФкВПЃЈВЛжЄУїЃЉЃП
ЃЈ2ЃЉЕБЕуFВЛдкBCЩЯЪБЃЌдкЭМЂкЁЂЭМЂлСНжжЧщПіЯТЃЈЩшEFЛђбгГЄЯпгыBCНЛгкPЃЌEGгыCAЛђбгГЄЯпНЛгкQЃЉЃЌЗжБ№аДГіOPгыOQЕФЪ§СПЙиЯЕЃЌВЂНЋЭМЂлЧщПіИјгшЫЕУїЃЎ
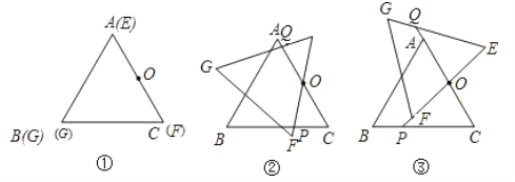
ЁОД№АИЁПЃЈ1ЃЉЕБ0ЁуЃМІСЃМ60ЁуЃЌЕуFдкЁїABCЕФЭтВПЃЛЕБІСЃН60ЁуЃЌЕуFдкBCЕФжаЕуЃЛЕБ60ЁуЃМІСЃМ120ЁуЃЌЕуFдкЁїABCЕФФкВПЃЛЃЈ2ЃЉСНжжЧщПіЯТОљгаOPЃНOQЃЛжЄУїМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉАДееІСЃН60ЁуЃЌ0ЃМІСЃМ60ЁуЃЌ60ЁуЃМІСЃМ120ЁуЗжРрЫЕУїЃЛ
ЃЈ2ЃЉРћгУASAЃЌбАевжЄУїШ§НЧаЮШЋЕШЕФЬѕМўЃЎ
НтЃКЃЈ1ЃЉЕБІС=60ЁуЪБЃЌШчЭМЂмЃЌ
ЁпЁЯCOF=60ЁуЃЌOЮЊACЃЌEFЕФжаЕуЃЌ
ЁрOF=OCЃЌ
ЁрЁїCOFЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯOCF=ЁЯACB=60ЁуЃЌ
ЁрЕуFдкBCБпЩЯЃЌ
ЕБІС=120ЁуЪБЃЌШчЭМЂнЃЌдђЁЯAOF=60ЁуЃЌ
ЁпOЮЊACЃЌEFЕФжаЕуЃЌ
ЁрOF=AOЃЌ
ЁрЁїAOFЮЊЕШБпШ§НЧаЮЃЌ
ЁрЁЯOAF=ЁЯCAB=60ЁуЃЌ
ЁрЕуFдкABБпЩЯЃЌ
ЁрЕБ0ЁуЃМІСЃМ60ЁуЃЌЕуFдкЁїABCЕФЭтВПЃЌ
ЕБІСЃН60ЁуЃЌЕуFдкBCЕФжаЕуЃЌ
ЕБ60ЁуЃМІСЃМ120ЁуЃЌЕуFдкЁїABCЕФФкВПЃЛ
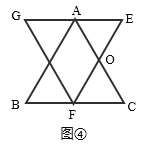
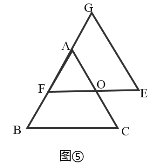
ЃЈ2ЃЉСНжжЧщПіЯТОљгаOPЃНOQЃЛ
жЄУїЃКШчЭМЂлЃЌгЩЬтвтПЩжЊЃКЁЯEЃНЁЯCЃН60ЁуЃЌOEЃНOCЃН![]() ACЃЌЁЯEOQЃНЁЯCOPЃЌ
ACЃЌЁЯEOQЃНЁЯCOPЃЌ
ЁрЁїEOQЁеЁїCOPЃЈASAЃЉЃЌ
ЁрOPЃНOQЃЎ